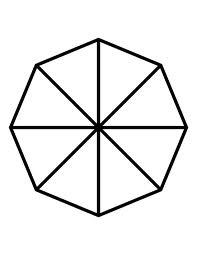
Octagon
We have a square with a side 56 cm. We cut corners to make his octagon. What will be the side of the octagon?
Correct answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- planimetrics
- Pythagorean theorem
- right triangle
- polygon
- triangle
- square
- diagonal
- goniometry and trigonometry
- sine
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Resulting cross
From the corners of the square with a side length of 10 cm, we cut out small squares with a side length of 3 cm. What is the area of the resulting cross? - Octagon from rectangle
We cut the corners of a rectangular tablecloth with dimensions of 4 dm and 8 dm into isosceles triangles. Thus, the octagon formed had an area of 26 dm². How many dm² of tablecloth do we cut down? - Regular octagon pad
You need to make a pad in the shape of a regular octagon with a side length of 4 cm. What is the minimum diameter of the circle-shaped semi-finished product from which we make the pad, and what will be the percentage of waste? (Round the results to 1 deci - Right-angled 66344
From a square with a side of 4 cm, we cut four right-angled isosceles triangles with right angles at the square's vertices and with an overlap of √2 cm. We get an octagon. Calculate its perimeter if the area of the octagon is 14 cm².
- Cube corners
From the cube of edge 5 cm, we cut off all vertices so that each cutting plane intersects the edges 1 cm from the nearest vertice. How many edges will this body have? - Decimetres 6341
We cut identical cubes with an edge length of 2 cm from two corners from a wooden cube with an edge of 0.6 decimetres. How many cubes with an edge length of 2 cm can still be cut from a wooden cube? - Cutting circles
From the square 1 m sides, we have to cut the circles with a radius of 10 cm. How many discs will we cut, and how many percent will be wasted?
