Squares
A square of 12 dm perimeter is cut into smaller squares, whose side is the third side of the square. What is the area of the rest?
Correct answer:
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- MO-Z5-3-66 tiles
The picture shows square tiles with a side of 10 dm, composed of four identical small rectangles and squares. The circumference of a small square is five times smaller than the circumference of the entire tile. Determine the dimensions of the rectangle. - Perimeter of the circle
Calculate the perimeter of the circle in dm, whose radius equals the side of the square containing 0.49 dm². - Cardboard box
Peter had square cardboard. The length of the pages was an integer in decimetres. He cut four squares with a side of 3 dm from the corners and made a box out of it, which fit precisely 108 cubes with an edge one dm long. Julia cut four squares with a side - Resulting cross
From the corners of the square with a side length of 10 cm, we cut out small squares with a side length of 3 cm. What is the area of the resulting cross?
- Squares
Cut out the square with the integer side from the square with the integer side so that the residual area is 100. What is the longest possible side of the larger square? - Rectangle 82740
A square in a grid contains 36 squares. This is one-fifth of the number of squares of a rectangle whose side is 30 squares long. What is the length of the other side of the rectangle? Thank you - Right-angled 66344
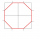From a square with a side of 4 cm, we cut four right-angled isosceles triangles with right angles at the square's vertices and with an overlap of √2 cm. We get an octagon. Calculate its perimeter if the area of the octagon is 14 cm².
