Three excursions
Each pupil of the 9A class attended at least one of the three excursions. There could always be 15 pupils on each excursion. Seven participants of the first excursion also participated in the second, 8 participants of the first excursion, and 5 participants of the second excursion also attended the third. Four pupils participated in all three excursions. How many pupils were in the 9A class?
Correct answer:
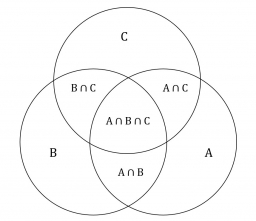
You need to know the following knowledge to solve this word math problem:
algebrabasic operations and conceptsnumbersGrade of the word problem
Related math problems and questions:
- Performances 2596
There were shows in the city cinema over the weekend. On Saturday, 12 students from our class participated in the performance, and on Sunday, 8 students participated. Fifteen pupils attended the performances. How many pupils attended both performances? - Students 6541
There are a total of 47 pupils in three classes in the rural school. There are 20% more pupils in the first grade than in the second grade and one pupil less in the third grade than in the second grade. How many students are there in each class? - Four classses
Students of all 7, 8, and 9 classes in one school may take up 4, 5, 6, and 7 abreast, and nobody will be left. If there are always four classes in each grade, what is the average number of pupils in one class? - Sports games
Pupils of the same school participated in district sports games. When dividing the teams into teams, it was found that in the case of the creative teams with four pupils, one pupil was remaining, five-member teams had two pupils, and six-member teams had - Dentist
Class 5. I participated in a preventive dental examination. A quarter of the pupils found two dental caries, and an eighth found one caries. Half the class had all their teeth healthy. How many students attend class 5? If four students were missing on the - Individual 28401
In the first and second years, there are 58 pupils in a pile. In the first and third years, there are 57 pupils. In the second and third years, there are 59 pupils. How many students are there: a) In all of them, to the dromedary, b) In individual classes - Participated 8264
Classes 1B, 2A, and 3C, participated in the volleyball tournament. How many ways could they take first, second, or third place? What is the probability that 1B will end before 2A class?
