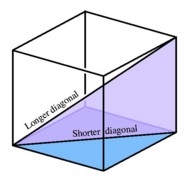
Space diagonal
The space diagonal of a cube is 129.91 mm. Find the lateral area, surface area, and volume of the cube.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Regular square prism
The volume of a regular square prism is 192 cm³. The size of its base edge and the body height is 1:3. Calculate the surface of the prism. - Sphere area
A cube with an edge 1 m long is a circumscribed sphere (vertices of the cube lie on a sphere's surface). Find the surface area of the sphere. - Diagonal 8192
Find the volume and surface of a cube if you know the length of its body diagonal u = 216 cm. - Body diagonal
Find the cube surface if its body diagonal has a size of 6 cm.
- Surface area of cylinder
Determine the lateral surface of the rotary cylinder, which is a circumscribed cube with a 5 cm edge length. - Cube wall
The perimeter of one cube wall is 120 meters. Calculate the surface area and the body diagonal of this cube. - Inscribed 81949
A cube is inscribed in a sphere with a radius of 27 cm. Calculate its volume and surface area.
