Land boundary
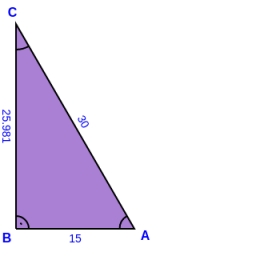
The land has the shape of a right triangle. The hypotenuse has a length of 30m. The circumference of the land is 72 meters. What is the length of the remaining sides of the land boundary?
Correct answer:
Tips to related online calculators
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Pythagorean theorem is the base for the right triangle calculator.
Do you want to convert length units?
See also our trigonometric triangle calculator.
Pythagorean theorem is the base for the right triangle calculator.
Do you want to convert length units?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Right triangle eq2
Find the lengths of the sides and the angles in the right triangle. Given area S = 210 and perimeter o = 70. - The sides
The sides of the rectangle are in a ratio of 3: 5 and its circumference measures 72 cm. Calculate: a) the size of both sides of the rectangle b) the area of the rectangle c) the length of the diagonals - ISO triangle
Calculate the area of an isosceles triangle KLM if its sides' length is in the ratio k:l:m = 4:4:3 and has perimeter 377 mm. - Garden
The area of a square garden is 2/9 of triangle garden with sides 160 m, 100 m, and 100 m. How many meters of fencing need to fence a square garden? - Harry
Harry Thomson bought a large land in the shape of a rectangle with a circumference of 90 meters. He divided it into three rectangular plots. The shorter side has all three plots of equal length, their longer sides are three consecutive natural numbers. Fi - Rectangle
The rectangle has a perimeter 75 cm. Diagonal length is 32.5 cm. Determine the length of the sides. - Right triangle eq2
Hypotenuse of a right triangle is 9 cm longer than one leg and 8 cm longer than the second leg. Determine the circumference and area of a triangle. - Rectangular garden
The sides of the rectangular garden are in ratio 1: 2. The diagonal has a length of 20 meters. Calculate the area and perimeter of the garden. - RT leg and perimeter
Calculate the length of the sides of a right triangle ABC with hypotenuse c when the length of a leg a= 84 and perimeter of the triangle o = 269. - Perimeter and legs
Determine the perimeter of a right triangle if the length of one leg is 75% length of the second leg and its content area is 24 cm². - Triangular prism
The base of the perpendicular triangular prism is a rectangular triangle with a hypotenuse of 10 cm and one leg of 8 cm. The prism height is 75% of the perimeter of the base. Calculate the volume and surface of the prism. - Triangular land
Jana has a rectangular garden measuring 30 meters by 72 meters that she wants to split diagonally from corner to corner using a fence. How long does her fence need to be? - Ratio of sides
Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in ratio 2 to 7. - Triangle - is RT?
Triangle has a circumference of 90 cm. Side b is 1 cm longer than c, and side c is 31 cm longer than side a. Calculate the length of sides and determine whether a triangle is a right triangle. - Equilateral triangle
Calculate the area of an equilateral triangle with circumference 72cm. - Difference of legs
In a right triangle, the length of the hypotenuse is 65 m, and the difference of legs is 23 m. Calculate the perimeter of this triangle. - Garden G
The rectangular, trapezoidal garden has a base length of 81m, 76m, and a vertical arm of 12m. Calculate how many m² of the area will remain for planting greenery if 1/3 of the area is built. Calculate the consumption of mesh for land fencing.
