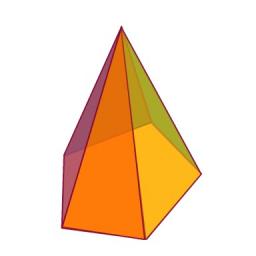
Pentagonal pyramid
Calculate the volume of a regular 5-side (pentaprism) pyramid ABCDEV; if |AB| = 7.7 cm and a plane ABV, ABC has angle 37 degrees.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Pyramid
The pyramid has a base a = 3cm and height in v = 15 cm. a) calculate the angle between plane ABV and the base plane b) Calculate the angle between the edges on the opposite side. - Triangular prism
The plane passing through the edge AB and the center of segment CC' of regular triangular prism ABCA'B'C' has an angle with base 30 degrees, |AB| = 15 cm. Calculate the volume of the prism. - Tetrahedral pyramid
Calculate the regular tetrahedral pyramid's volume and surface if the area of the base is 20 cm² and the deviation angle of the side edges from the plane of the base is 60 degrees. - 4side pyramid
Calculate the volume and surface of the regular four-sided pyramid whose base edge is 4 cm long. The angle from the plane of the sidewall and base plane is 60 degrees.
- Quadrilateral pyramid
The regular quadrilateral pyramid has a base edge a = 1.56 dm and a height h = 2.05 dm. Calculate: a) the deviation angle of the sidewall plane from the base plane b) deviation angle of the side edge from the plane of the base - Quadrilateral 6353
Given is a regular quadrilateral pyramid with a square figure. Side = 16 cm, S = 736 cm². Calculate h (body height) and body volume V. - Truncated pyramid
Find the volume of a regular 4-sided truncated pyramid if a1 = 14 cm, a2 = 8 cm, and the angle that the side wall with the base is 42 degrees.
