Exponential equation
Solve exponential equation (in real numbers):
23x-6=9
23x-6=9
Correct answer:
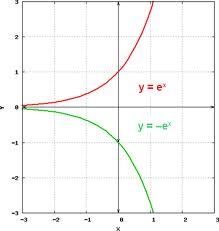
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebrabasic operations and conceptsnumbersGrade of the word problem
Related math problems and questions:
- Coordinate
Determine the unknown coordinate of the point M [x, 54] of the graph of the function f by rule: y = 3x - Equations: 80499
In the field of real numbers, solve the system of equations: 2x + ⌊y⌋ = 2022, 3y + ⌊2x⌋ = 2023. (⌊a⌋ denotes the (lower) integer part of the real number a, i.e., the largest integer not greater than a., E.g., ⌊1.9⌋ = 1 and ⌊−1.1⌋ = −2.) - Logarithmic equation
Solve equation: log13(7x + 12) = 0 - Biquadratic
By introducing a new variable, solve the biquadratic equation: - x 4 +277 x² -15876=0
In the set R, solve the equation: 7 -5 +19x=4 3 -20x
Solve the equation and check the result: 1.6x - 3/2 + x - 9,8 = x + 0,4/3 - 7 + 1,6/6
Solve the exponential equation: 8 raised to x = 40