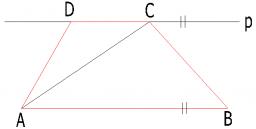
Trapezoid v3
The isosceles trapezoid has an angle at the first base 40 degrees less than the angle at the second base. How large angles has this trapezoid?
Your answer:
Your answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebraplanimetryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Triangle angle
An isosceles triangle has the size of the angles at the base alpha = beta = 34 degrees 34 minutes. Calculate the magnitude of the angle at the remaining vertex of the triangle in degrees and minutes. - Triangle angle calculation
The outside angle at the base of an isosceles triangle is 132 degrees. Calculate the angles of a triangle internally. - An isosceles trapezoid
An isosceles trapezoid has base angles of 50° each, and its bases are 20 cm and 30 cm. Compute its area. - Inner angles
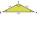The magnitude of the internal angle at the central vertex C of the isosceles triangle ABC is 72°. The line p, parallel to the base of this triangle, divides the triangle into a trapezoid and a smaller triangle. How big are the inner angles of the trapezoi - Drawing Similar Triangle
Isosceles triangle X'Y'Z' . It is similar to triangle XYZ. The base of triangle XYZ has length |XY|=4 cm. The size of the angle at the X vertex is 45 degrees. Draw a triangle X'Y'Z' whose base is 8 cm long. - Triangle area calculation
The isosceles triangle XYZ has a base of z = 10 cm. The angle to the base is the sum of the angles at the base. Calculate the area of the triangle XYZ. - ISO trapezium
Calculate the area of an isosceles trapezoid with base 50 long, leg 12 long, and with the angle between the base and leg 70 degrees.
