Similarity of squares
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
geometryalgebraarithmeticplanimetricsbasic operations and conceptsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- The 8th
The 8th term of GP is greater than the 5th term, and the 10th term is 10 times the 2nd term find: 1) the common ratio 2) 20th term - Isosceles trapezoid
Perimeter of the isosceles trapezoid is 48 cm. One side is two times greater than the second side. Determine the dimensions of the trapezoid. - Circumscribed - sphere
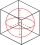A cube with a volume of 4096 cm³ is described and inscribed by a sphere. Calculate how many times the volume of the circumscribed sphere is greater than the inscribed sphere. - 3x square
The side length of the square is 54 cm. How many times does a square's area increase if the side's length increases three times? - Difference 68514
How many times is the difference between the squares of numbers 4 and 2 bigger than the square of their difference (in this order)? - One side 2
One side of the rectangle is three times larger, and the other is 4 cm smaller than the side of the square. Find the area of the square if more than the area of the rectangle by 10 cm². - Unknown number
I think number. If I subtract from the twelfth square the ninth square, I get a number 27 times greater than the intended number. What is this unknown number?
