Intersections 25141
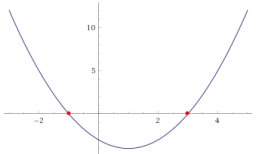
The quadratic function has the formula y = x²-2x-3. Sketch a graph of this function. Find the intersections with the axes. Find the vertex coordinates.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
Grade of the word problem:
Related math problems and questions:
- Intersections 80587
Draw the graph of the function y = -2x + 3. Calculate the coordinates of the intersections of the function's graph with the x and y axes. - Intersections 49433
Draw a graph of the function given by the equation y = -2x +3, determine its intersections with the coordinate axes, and complete the missing coordinates A [3;? ], B [?; 8]. - Intersections 62534
The equation of the linear function is: y = -3x + 4 (a) determine the intersections with the axes sketch chart b) for which x applies f (x) = - 1 c) for which x applies f (x) = 0 d) for which y applies f (-1/2) = y - Intersections
Find the intersections of the function plot with coordinate axes: f (x): y = x + 3/5
- Intersections 62784
A quadratic function is given: y = -x² + 2x + 3 a) determine the intersections with the x, y-axis and peak V b) draw a graph and describe c) for which x applies f (x) = 3 - Parabola with abs
A). Sketch the graph of the function f(x)=x * absolute(x) = x * |x| b). For what values of x is f(x) differentiable c). Find F(x) - Intersections 2574
Calculate the intersections with the x and y axes of the function h: y = 4 / 5x-3
