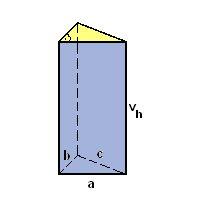
Prism
Find the volume and surface area of a prism with a base of an equilateral triangle with a side of 7 dm long and a body height of 1.5 m.
Correct answer:
Tips for related online calculators
Do you know the volume and unit volume, and want to convert volume units?
The Pythagorean theorem is the base for the right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
The Pythagorean theorem is the base for the right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Prism - eq triangle
Calculate the volume and surface of the prism with the base of an equilateral triangle with side a = 4cm and the body height is 6cm. - Perpendicular 35183
Calculate the surface and volume of a vertical prism if its height h = 18 cm and if the base is an equilateral triangle with side length a = 7.5 cm. - Right-angled triangle base
Find the volume and surface area of a triangular prism with a right-angled triangle base if the length of the prism base legs are 7.2 cm and 4.7 cm and the height of a prism is 24 cm. - Find the Find the volume and surface of a prism with a height of 120 mm, the base of which is a right isosceles triangle with a leg length of 5 cm.
- Triangular prism
Calculate the surface of a triangular prism with the base of an equilateral triangle with a side length of 7.5 cm and a corresponding height of 6.5 cm. Prism height is 15cm. - The height of prism
A right triangle forms the base of the perpendicular prism with perpendiculars 30 cm and 40 cm long. This prism has the same volume as a cube with an edge length of 3 dm. Find its height in cm. - Perpendiculars 2756
Determine the volume and surface of a prism with the base of a right triangle if the perpendiculars are: a is 1.2 cm. b is 2cm. The height of the body is 0.3 dm. - Tetrahedral pyramid
Calculate the surface S and the volume V of a regular tetrahedral pyramid with the base side a = 5 m and a body height of 14 m. - Triangular prism
The regular triangular prism has a base edge of 8.6 dm and a height of 1.5 m. Find its volume and surface area. - Triangular prism
Calculate the volume and surface area of a triangular prism if it is given: a = 6.8 dm. ..Va = 4 dm. (base edge length and base triangle height length) ... ... .v = 23 dm (body height) - Equilateral 2714 Determine the volume and surface of a 9 cm high triangular prism if the base is an equilateral triangle with a side of 8 cm.
- Largest wall
Find the area of the largest wall of a prism with a rectangle base with a height of 4 dm, side c = 5 cm, and side b = 6 cm. - A regular
A regular triangular prism with a base edge of 20 dm and a height of 30 dm is drawn. Find the volume of the prism and the area of the shell. - Hexagonal prism
Calculate the volume and surface of a regular hexagonal prism with the edge of the base a = 6 cm with the corresponding height v1 = 5.2cm and the height of the prism h = 1 dm. - Triangular prism - regular
The regular triangular prism is 7 cm high. Its base is an equilateral triangle whose height is 3 cm. Calculate the surface and volume of this prism. - Triangular prism
The base of the perpendicular triangular prism is a right triangle with a leg length of 5 cm. The area of the largest sidewall of its surface is 130 cm², and the body's height is 10 cm. Calculate its volume. - Hexagonal prism
The prism's base is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism.
