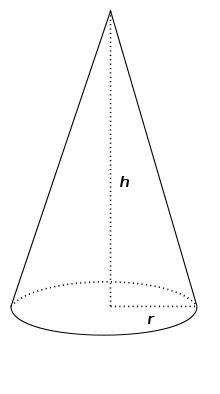
Cone container

The Rotary cone-shaped container has a volume of 1000 cubic cm and a height of 12 cm. Calculate how much metal we need to make this package.

Your answer:

Help us improve! If you spot a mistake, please let let us know. Thank you!

Tips for related online calculators

Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.

You need to know the following knowledge to solve this word math problem:

algebra

rearrange variables

solid geometry

cone
surface area

planimetry

Pythagorean theorem
right triangle
triangle

Units of physical quantities

volume

Grade of the word problem

practice for 14 year olds
high school

We encourage you to watch this tutorial video on this math problem: video1 video2

Related math problems and questions:

Rotary cone
A rotary cone whose height is equal to the circumference of the base has a volume 2488 cm³. Calculate the radius of the base circle and the height of the cone.
Cube-shaped container
The cube-shaped container has a height of 52 cm and a square base. The container was filled to the brim with water, and then we immersed a metal cube in it, which caused 2.7 l of water to flow out of the container. After removing the cube from the water,
The cylindrical container
The cylindrical container has a base area of 300 cm³ and a height of 10 cm. It is 90% filled with water. We gradually insert metal balls into the water, each with a volume of 20 cm³. After inserting, how many balls does water flow over the edge of the con
Metal sheet
Calculate how much sheet metal is needed to make a closed block-shaped container with dimensions of 2 m, 7 m, and 9 m if we must add 12% to the welds.
Rotary bodies
The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area?
Lamp cone
Calculate the surface of a lampshade shaped like a rotary truncated cone with a base diameter of 32 cm and 12 cm and a height of 24 cm.
Ice Cream Cones Volume
How many cone-shaped cones will we have to take to fill 20 l of creams (to the brim) if the cone has an inner base diameter of 6 cm and a height of 8 cm. Make a drawing, and write the answer.