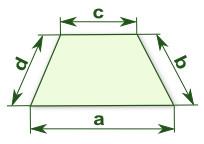
Four sides of trapezoid
The trapezoid is given by the length of four sides: 40.5, 42.5, 52.8 35.0. Calculate its area.
Correct answer:
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Calculate: 36721
In the trapezoid, it is given: all four sides a = 51 cm; b = 30 cm; c = 18 cm; d = 27 cm; and height v = 24 cm; Calculate: perimeter o=? and area S=? - Calculated: 2839
A trapezoid is given: c = 4.2 cm, h = 8 cm, S = 42.4 cm, d = 8.4 It would help if you calculated the following: sides a and b, and perimeter o: - Parallelogram 6385
The parallelogram is given by: a, b is adjacent sides, va, vb - the respective heights to the individual sides. Calculate its side a, if b = 6cm, va = 3cm, vb = 4cm - Four sides of trapezoid
Calculate the area of the ABCD trapezoid with sides a = 65 cm, b = 29 cm, c = 40 cm, d = 36 cm
- Trapezoid
The rectangular trapezoid ABCD with a right angle at the vertex A has sides a, b, c, and d. Calculate the circumference and the area of the trapezoid if given: a = 25cm, c = 10cm, d = 8cm - Isosceles trapezoid
Isosceles trapezoid ABCD, AB||CD is given by |CD| = c = 12 cm, height v = 5 cm and |CAB| = 41°. Calculate area of the trapezoid. - Parallelogram 65334
In a parallelogram, the sum of the lengths of the sides a+b = 234. The angle subtended by the sides a and b is 60°. The diagonal size against the given angle of 60° is u=162. Calculate the sides of the parallelogram, its perimeter, and its area.
