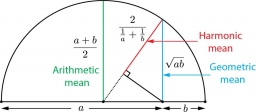
Harmonic mean
If x, y, and z form a harmonic progression, y is the harmonic mean of x and z. Find the harmonic mean of the numbers 6 and 5.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
statisticsalgebrabasic operations and conceptsGrade of the word problem
Related math problems and questions:
- Harmonic series
Insert four members between 5/3 and 5/11 to form a harmonic series (means). - HP - harmonic progression 2
Compute the 16th term of the HP if the 6th and 11th terms of the harmonic progression are 10 and 18, respectively. - HP - harmonic progression
Determine the 10th term of the harmonic progression 6,4,3,… - The terms
The terms 1/64, 1/32, and 1/16 form a geometric progression (GP). If the sum of the GP is (2³6 – 2-6), find the number of terms. - Harmonic 4 Find the harmonic mean of -6 and 5.
- The lengths
The lengths of the twelve poles form an Arithmetic Progression (A. P). If the third pole is 3m and the eighth pole is 5 m, find the (i) Length of the first pole (ii) Sum of the length of the poles - Insert 5
Insert five harmonic means between 1/2 and 1/26
