The terms
The terms 1/64, 1/32, and 1/16 form a geometric progression (GP). If the sum of the GP is (236 – 2-6), find the number of terms.
Final Answer:
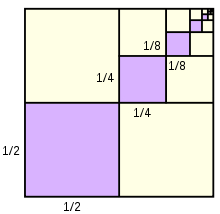
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticbasic operations and conceptsnumbersGrade of the word problem
Related math problems and questions:
- Sum of GP members
Determine the sum of the GP 30, 6, 1.2, to 5 terms. What is the sum of all terms (to infinity)? - GP - sequence
The first three terms of a geometric sequence are as follows: 10, 30, 90. Find the next two terms of this sequence. - Six terms GP
Find the sum of the six terms of the finite geometric sequence 96, -48, 24, -12 - In a GP 72+144 In a GP, the sum of the 2nd and fifth terms is 72, and the sum of the 3rd and 6th terms is 144. Find the common ratio, find the first term, and find the sum of the first six terms
- Insert into GP
Between numbers 5 and 640, insert as many numbers as necessary to form a geometric progression, so the sum of the numbers you entered will be 630. How many numbers must you insert? - Two geometric progressions
Insert several numbers between numbers 6 and 384 so that they form with the given GP numbers and that the following applies: a) the sum of all numbers is 510 And for another GP to apply: b) the sum of entered numbers is -132 (These are two different geome - The sum 53
The sum ofthree numbers of a GP series is 35 and their product is 1000. Find the numbers.
