The base 2
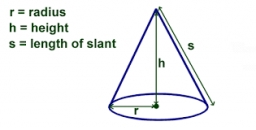
The base diameter of a right cone is 16cm, and its slant height is 12cm.
A. ) Find the perpendicular height of the cone to 1 decimal place.
B. ) Find the volume of the cone, and convert it to 3 significant figures. Take pi =3.14
A. ) Find the perpendicular height of the cone to 1 decimal place.
B. ) Find the volume of the cone, and convert it to 3 significant figures. Take pi =3.14
Correct answer:
Showing 1 comment:
Student
In B you used pi to more significant digits than just three. If I used 3.14 I get a different answer. Also with the other figueres used. The question needs to be more specific about what figures to use in the calculation? Thanks for a good practice though!
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- arithmetic
- square root
- solid geometry
- cone
- planimetrics
- Pythagorean theorem
- right triangle
- numbers
- fractions
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- The diagram 2
The diagram shows a cone with a slant height of 10.5cm. If the curved surface area of the cone is 115.5 cm². Calculate to correct three significant figures: *Base Radius *Height *Volume of the cone - Calculating 63344
Calculate the volume of the cone formed by rotating an isosceles triangle about the height of the base. The triangle has a side length of 15 cm and a height to the base of 12 cm. When calculating, use the value pi = 3.14 and round the result to one decima - The radius
A right circular cone's radius and slant heights are 9 cm and 15 cm, respectively. Find, correct to one decimal place, the (i) Height (ii) Volume of the cone - Slant height
Find the cone's volume. The cone's slant height is 5cm, and the radius of its base is 3cm.
- A cone 2 A cone has a slant height of 10 cm and a square curved surface area of 50 pi cm. Find the base radius of the cone.
- Pile of sand
A large pile of sand has been dumped into a conical pile in a warehouse. The slant height of the pile is 20 feet. The diameter of the base of the sandpile is 31 feet. Find the volume of the pile of sand. - Slant height 3
The frustum of a right circular cone has the diameters of base 10 cm of top 6 cm and a height of 5 cm. Find the slant height.
