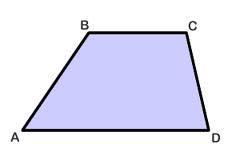
Trapezoid
Calculate the area of trapezoid ABCD with sides |AB|= 78 cm, |BC|=51 cm, |CD|=15 cm, |AD|=30 cm..
Final Answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you want to round the number?
See also our trigonometric triangle calculator.
Do you want to round the number?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsGrade of the word problem
Related math problems and questions:
- Trapezoidal prism
Calculate the surface of the quadrilateral prism ABCDA'B'C'D' with the trapezoidal base ABCD. The height of the prism is 12 cm; ABCD trapezoidal data: AB base length is 8 cm, CD base length is 3 cm, BC arm length is 4 cm, and AC diagonal length is 7 cm. L - Trapezoid: 18703
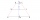In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle. - Circumference 7052
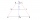The trapezoid ABCD is given (AB || CD, AB perpendicular to AD). Calculate its circumference if | AB | = 20cm, | CD | = 15cm, | AD | = 12cm. Pythagorean theorem - Diagonal
The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm and CD = 4cm. Calculate the length of the AC diagonal. - Isosceles 37621
In the isosceles trapezoid ABCD, its bases AB = 20cm, CD = 12cm and arms AD = BC = 8cm are given. Specify its height and alpha angle at vertex A - Quadrilateral 80729
Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD. - Triangle ABP
An isosceles trapezoid ABCD is given. The length of side AB is 10 cm, the length of CD is 7 cm, and the height to side AB is 4 cm. Point P is the base of the altitude to side AD. Calculate the area of the triangle ABP.
