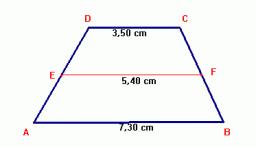
Trapezoid - central median
The central median divides the trapezoid into two smaller trapezoids. Find the ratio of its areas.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsbasic operations and conceptsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Length 26
The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is: - Coat of arms
The class created its coat of arms, which had a shape composed of an isosceles trapezoid ABCD (shorter base is a = 4.5 cm long, longer 2a = 9 cm, trapezoid height 6 cm) and a semicircle with center S and diameter AB. Three identical isosceles triangles fo - Inner angles
The magnitude of the internal angle at the central vertex C of the isosceles triangle ABC is 72°. The line p, parallel to the base of this triangle, divides the triangle into a trapezoid and a smaller triangle. How big are the inner angles of the trapezoi - Chord 24
A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments?
- The sides 2
The sides of a trapezoid are in the ratio 2:5:8:5. The trapezoid's area is 245. Find the height and the perimeter of the trapezoid. - Trapezoids
In the isosceles trapezoid ABCD we know: AB||CD, |CD| = c = 8 cm, height h = 7 cm, |∠CAB| = 35°. Find the area of the trapezoid. - Trapezoid thirds
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment.
