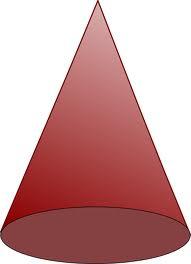
Rotation
The right triangle with legs 11 cm and 18 cm rotates around the longer leg.
Calculate the volume and surface area of the formed cone.
Calculate the volume and surface area of the formed cone.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetricsnumbersUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Perpendiculars 36213
A right triangle with perpendiculars a = 3 cm and b = 4 cm rotates around a longer perpendicular. Calculate the volume and surface area of the resulting cone. - Triangle and Cone
A right triangle has legs 3 cm and 4 cm long. One cone (let's call it A) was created by rotating this triangle around the long leg, and the other (let's call it B) by rotating it around the shorter leg. Which cone has: a) a larger volume b) a smaller surf - Resulting 4446
A square with a side length of 3 cm rotates around its diagonal. Calculate the volume and surface area of the resulting body. - Calculate
Calculate the cone's surface and volume from the rotation of the right triangle ABC with the squares 6 cm and 9 cm long around the shorter squeegee.
- RT area
A right triangle has an area of 54cm². Calculate the sizes of both legs if the shorter leg is 75% of the size of the longer leg. - Perpendicular legs PT
In a right triangle, one leg is 5 cm longer than the other leg. The hypotenuse is 150 mm. Calculate the lengths of the legs. - Perpendiculars 17003
What is the hole volume drilled by the drill in the shape of a right triangle that revolves around a longer perpendicular? The perpendiculars of the triangle are 10 cm and 3 cm long.
