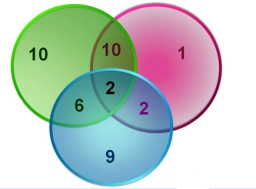
Three subjects
In a class of 40 students, 18 passed mathematics, 19 passed accounting, 16 passed economics, five mathematics and accounting only, six mathematics only, nine accounting only, and two accounting and economics only. Each student was offered at least one of the subjects.
a) how many students failed in all the subjects?
b) find the percentage number who failed in at least one of economics and mathematics.
c) calculate the probability that a student selected at random failed in accounts
Your answer:
a) how many students failed in all the subjects?
b) find the percentage number who failed in at least one of economics and mathematics.
c) calculate the probability that a student selected at random failed in accounts
Your answer:
Tips for related online calculators
Our percentage calculator will help you quickly and easily solve a variety of common percentage-related problems.
Would you like to compute the count of combinations?
Would you like to compute the count of combinations?
You need to know the following knowledge to solve this word math problem:
combinatoricsalgebrabasic operations and conceptsGrade of the word problem
Related math problems and questions:
- Students and exam
In a certain college, accounting is one of the courses. Among the accounting students, 60% are male. Among the male students, 75% passed the exams, while among the female students, 50% failed. (a) Present this information using a probability tree diagram. - Failed in examination
In an examination, 20% of the total students failed in history, 15% failed in English, and 5% of the total number of students failed in both subjects. Find the percentage of the total number of students who passed in both subjects. - Award
Out of 36 students, 16 were awarded, 19 passed, 1 failed. Determines the percentage of honors and successful students in the class. - An examination
In an examination 65% students passed in English and 56% in mathematics. And 25% failed in both the subjects. If 414 passed in both the subjects, then find the total number of students. - Testing students
Giving a test to a group of students, the grades and gender are summarized below. Grades and Gender ; A; B ; C ; Total Male; 20; 6; 19 ; 45 Female ; 17; 18; 13; 48 Total; 37; 24; 32; 93 If one student is chosen at random, a) Find the probability that the - Student grade percentage There are 32 students in the class; 17 are awarded, 14 passed, and 1 failed. Determine the number percentages of students with honors, successful and not successful students
- In class 24
There are a total of 16 students in the class, a quarter of whom are girls. A team of five is selected at random. Determine the probability that the team will have: a) at least 4 girls, b) at most 1 girl, c) no girls.
