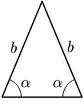
Triangle TBC
TBC is an isosceles triangle with base TB with base angle 75° and legs length |TC| = |BC| = 35. How long is the base TB?
Final Answer:
Tips for related online calculators
Calculation of an isosceles triangle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
planimetricsnumbersgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- IS triangle
Calculate the interior angles of the isosceles triangle with base 12 cm and legs 19 cm long. - Triangle's centroid
In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t - Isosceles 71154
Calculate all interior angles in the isosceles triangle ABC if we know that BC is the base, and we also know: | ∢BAC | = α; | CABCA | = 4α - Main/central vertex ABC is an isosceles triangle with base BC and central vertex A. The angle at vertex A is 18°. What will be the size of the angle at vertex B?
- Circle inscribed
There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26? - Medians of isosceles triangle
The isosceles triangle has a base ABC |AB| = 16 cm and a 10 cm long arm. What is the length of the medians? - Calculate 4425
In the triangle ABC with the center of gravity T, b = 7cm, median to c: tc = 9cm, the ATC angle is 112 degrees. Calculate the length of the line ta.
