Center of gravity and median
In the isosceles triangle ABC, the center of gravity T is 2 cm from the base AB. The median parallel to the AB side measures 4 cm. What is the area of the ABC triangle?
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Perimeter 6002
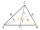In the triangle ABC there is a side c = 5cm and a medians ta = 6cm (median to side a), tb = 4.5cm (median to side b). Find the perimeter of the triangle ABT (T = center of gravity). - Medians 2:1
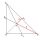The Median to side b (tb) in triangle ABC is 12 cm long. a. What is the distance of the center of gravity T from vertex B? b, Find the distance between T and the side b. - Center of gravity
In the isosceles triangle ABC is the ratio of the lengths of AB and the height to AB 10:12. The arm has a length of 26 cm. If the center of gravity is T, find the area of the triangle ABT. - Calculate 4425
In the triangle ABC with the center of gravity T, b = 7cm, median to c: tc = 9cm, the ATC angle is 112 degrees. Calculate the length of the line ta. - Isosceles 5575
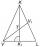The picture shows an isosceles triangle VLK with a center of gravity of T. The base VL measures 16 cm, and the line KK1 measures 18 cm. How long is the VV1 line? - Construction
Construct the triangle ABC if you know: the size of the side AC is 6 cm, the size of the angle ACB is 60°, and the distance of the center of gravity T from the vertex A is 4 cm. (Sketch, analysis, notation of construction, construction) - Ratio of triangles areas
In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas - Isosceles triangle
Calculate the area and perimeter of an isosceles triangle ABC with base AB if a = 6 cm, c = 7 cm. - Centre of mass
The vertices of triangle ABC are from the line p distances 3 cm, 4 cm, and 8 cm. Calculate the distance from the center of gravity of the triangle to line p. - There
There is a triangle ABC: A (-2,3), B (4, -1), C (2,5). Determine the general equations of the lines on which they lie: a) AB side, b) height to side c, c) Axis of the AB side, d) median ta to side a - Triangle 69144
The line p passes through the center of gravity T of the triangle and is parallel to the line BC. What is the ratio of the area of the divided smaller part of the triangle by the line p? What is the area of the triangle? - Isosceles 48443
Three equal positive charges Q are located at the vertices of an isosceles right triangle ABC. The right angle is at vertex A. The length of side AB is 1m. What is the electric field strength at the center S of side BC, i.e., what force would act on a pos - Segment in a triangle
In a triangle ABC with the side/AB/ = 24 cm constructed middle segment/DE/ = 18 cm parallel to the side AB at a distance of 1 cm from AB. Calculate the height of the triangle ABC to side AB. - Isosceles triangle
Calculate the height of the isosceles triangle ABC with the base AB, AB = c = 10 cm, and the arms a = b = 13 cm long. - Geodesist
Triangle-shaped field (triangle ABC) has a side AB = 129 m. path XY is parallel to the side AB, which divides triangle ABC into two parts with the same area. What will be the length of path XY? Help, please, geodesist. - Triangle ABC
In a triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC triangle A - Equilateral 5571
The height in the equilateral triangle ABC measures the square root of 3 cm. What is the length of the center bar of this triangle?
