Center of gravity
In the isosceles triangle ABC the lengths of AB and the height to AB is the ratio of 10:12. The arm has a length of 26 cm. If the center of gravity is T, find the area of the triangle ABT.
Final Answer:
Tips for related online calculators
Check out our ratio calculator.
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
planimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Perimeter triangle
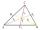 In the triangle ABC, there is a side c = 5cm and medians ta = 6cm (median to side a), tb = 4.5cm (median to side b). Find the perimeter of the triangle ABT (T = center of gravity).
In the triangle ABC, there is a side c = 5cm and medians ta = 6cm (median to side a), tb = 4.5cm (median to side b). Find the perimeter of the triangle ABT (T = center of gravity). - Center of gravity and median
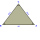 In the isosceles triangle ABC, the center of gravity T is 2 cm from the base AB. The median parallel to the AB side measures 4 cm. What is the area of the ABC triangle?
In the isosceles triangle ABC, the center of gravity T is 2 cm from the base AB. The median parallel to the AB side measures 4 cm. What is the area of the ABC triangle? - Ratio of triangles areas
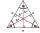 In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas
In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas - Right-angled 81019
 In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC.
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC. - Medians 2:1
 The Median to side b (tb) in triangle ABC is 12 cm long. a. What is the distance of the center of gravity T from vertex B? b, Find the distance between T and the side b.
The Median to side b (tb) in triangle ABC is 12 cm long. a. What is the distance of the center of gravity T from vertex B? b, Find the distance between T and the side b. - Arm
 Calculate the length of the arm r of isosceles triangle ABC, with base |AB| = 14 cm and a height v=18 cm.
Calculate the length of the arm r of isosceles triangle ABC, with base |AB| = 14 cm and a height v=18 cm. - Isosceles triangle
 What are the angles of an isosceles triangle ABC if its base is long a=7 m and has an arm b=9 m?
What are the angles of an isosceles triangle ABC if its base is long a=7 m and has an arm b=9 m?
