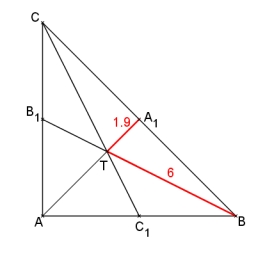
Medians 2:1
The Median to side b (tb) in triangle ABC is 12 cm long.
a. What is the distance of the center of gravity T from vertex B?
b, Find the distance between T and the side b.
a. What is the distance of the center of gravity T from vertex B?
b, Find the distance between T and the side b.
Correct answer:
Showing 2 comments:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Check out our ratio calculator.
Do you want to convert length units?
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Check out our ratio calculator.
Do you want to convert length units?
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Perimeter 6002
In the triangle ABC, there is a side c = 5cm and medians ta = 6cm (median to side a), tb = 4.5cm (median to side b). Find the perimeter of the triangle ABT (T = center of gravity). - Construction
Construct the triangle ABC if you know: the size of the side AC is 6 cm, the size of the angle ACB is 60°, and the distance of the center of gravity T from the vertex A is 4 cm. (Sketch, analysis, notation of construction, construction) - Center of gravity and median
In the isosceles triangle ABC, the center of gravity T is 2 cm from the base AB. The median parallel to the AB side measures 4 cm. What is the area of the ABC triangle? - Center
In the ABC triangle is point D[1,-2,6], which is the center of the |BC|, and point G[8,1,-3], which is the center of gravity of the triangle. Find the coordinates of the vertex A[x,y,z].
- Calculate 4425
In the triangle ABC with the center of gravity T, b = 7cm, median to c: tc = 9cm, the ATC angle is 112 degrees. Calculate the length of the line ta. - Median
In the ABC triangle is given side a=10 cm and median to side a: ta= 13 cm, and angle gamma 90°. Calculate the length of the median to side b (tb). - Centre of mass
The vertices of triangle ABC are from the line p distances 3 cm, 4 cm, and 8 cm. Calculate the distance from the center of gravity of the triangle to line p.
