Right-angled 5804
We sorted the lengths of the sides of the two triangles by size: 8 cm, 10 cm, 13 cm, 15 cm, 17 cm, and 19 cm. One of these two triangles is right-angled. Calculate the perimeter of this right triangle in centimeters
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Right-angled 64084
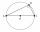A right-angled triangle ABC with sides 5 cm and 12 cm is described by circle k. Calculate the length of circle k in centimeters. When calculating, use π = 3, 14 and round the result to tenths. - Right angled triangle
The hypotenuse of a right triangle is 17 cm long. When we decrease the length of the legs by 3 cm, then decrease its hypotenuse by 4 cm. Find the size of its legs. - Circumference 42471
The lengths of the sides of the triangle ABC are in the ratio 4:2:5. Calculate the size of the longest side of a similar KLM triangle, whose circumference is 66 cm. - Right-angled 40961
A right-angled triangle ABC has sides a = 5 cm, b = 8 cm. The similar triangle A'B'C' is 2.5 times smaller. Calculate what percentage of the area of triangle ABC is the area of triangle A'B'C'. - Rectangular triangles
The lengths of corresponding sides of two rectangular triangles are in the ratio 2:5. At what ratio are medians relevant to hypotenuse these right triangles? At what ratio are the areas of these triangles? A smaller rectangular triangle has legs 6 and 8 c - Sides of right angled triangle
One leg is 1 m shorter than the hypotenuse, and the second leg is 2 m shorter than the hypotenuse. Find the lengths of all sides of the right-angled triangle. - Cuboid face diagonals
The lengths of the cuboid edges are in the ratio 1:2:3. Will the lengths of its diagonals be in the same ratio? The cuboid has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this cuboid. - Right triangles
How many right triangles we can construct from line segments 3,4,5,6,8,10,12,13,15,17 cm long? (Do not forget the triangle inequality). - Probability 7991
We have the numbers 4, 6, 9, 13, and 15. What is the probability that these will be the lengths of the sides of the triangle? (Consider only scalene triangles.) - Triangle ABC
In a triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC triangle A - Right-angled 66344
From a square with a side of 4 cm, we cut four right-angled isosceles triangles with right angles at the square's vertices and with an overlap of √2 cm. We get an octagon. Calculate its perimeter if the area of the octagon is 14 cm². - Calculate 60423
In a right triangle RST with a right angle at the vertex T, we know the lengths of two sides: s = 7.8 cm and t = 13 cm; calculate the third party r. - Calculate 72624
The perimeter of the ABC triangle is 19.6 cm. The following applies to the lengths of its sides: a: c = 1:2, b: c = 5:6. Calculate the lengths of all sides of the triangle ABC. - Conical area
A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation. - Two similar
Two similar triangles, one has a circumference of 100 cm, the second has sides successively 8 cm, 14 cm, and 18 cm longer than the first. Find the lengths of its sides. - Similarity of triangles
If triangle ABC ~ to triangle XYZ, AC = 24, AB = 15, BC = 17, and XY = 9, what is the perimeter of triangle XYZ? Round all sides to 1 decimal place. - Right-angled 81019
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC.
