Bamboo

At a certain height, the wind broke the bamboo high 32 feet, so the bamboo top reached the ground at a distance of 16 feet from the trunk. At what height from the ground was the bamboo broken?

Your answer:

Help us improve! If you spot a mistake, please let let us know. Thank you!

Tips for related online calculators

Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.

You need to know the following knowledge to solve this word math problem:

algebra

quadratic equation
equation
rearrange variables

planimetry

Pythagorean theorem
right triangle
triangle

Grade of the word problem

practice for 13 year olds
practice for 14 year olds
high school

We encourage you to watch this tutorial video on this math problem: video1 video2

Related math problems and questions:

A mast
The wind broke a mast 32 meters high so that its top touched the ground 16 meters from the pole. The still-standing part of the mast, the broken part, and the ground form a rectangular triangle. At what height was the mast broken?
Gale and spruce
A mighty gale broke the top of the fifteen-year spruce, resting it on the ground. The distance of this top from the trunk was 4.6 m below. At what height was the spruce trunk broken?
Spruce
A massive storm broke the top of a 15-metre spruce tree so that it remained hanging along the rest of the trunk. The tip of the broken top touched the ground 4.6 m from the base of the tree. At what height from the ground did the trunk break?
Broken tree
The tree is broken at 4 meters above the ground. The top of the tree touches the ground at a distance of 5 meters from the trunk. Calculate the original height of the tree.
Broken tree
The tree was 35 meters high. The tree broke at a height of 10 m above the ground. Top, but does not fall off. It is refuted on the ground. How far from the base of the tree lay its peak?
A tree 3
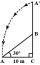A tree breaks due to a storm and the broken part bends so that the top of the tree touches the ground at an angle of 30°. The distance from the foot of the tree to the point where the top touches the ground is 8 m. Find the original height of the tree.
Tree breaking height
The 30-meter tree broke. Its top fell 5 m from the trunk. At what level did it break?