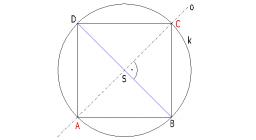
ABCD square
In the ABCD square, the X point lies on the diagonal AC. The length of the XC is three times the length of the AX segment. Point S is the center of the AB side. The length of the AB side is 1 cm. What is the length of the XS segment?
Final Answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Trapezoid thirds
 The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment.
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment. - Distance 64804
 Dan is the square ABCD. At its diagonal AC lies point E. The distance AB is equal to the distance AE. What is the size of the EBC angle?
Dan is the square ABCD. At its diagonal AC lies point E. The distance AB is equal to the distance AE. What is the size of the EBC angle? - Square ABCD
 Construct a square ABCD with center S [3,2] and the side a = 4 cm. Point A lies on the x-axis. Construct a square image in the displacement given by oriented segment SS'; S` [-1 - 4].
Construct a square ABCD with center S [3,2] and the side a = 4 cm. Point A lies on the x-axis. Construct a square image in the displacement given by oriented segment SS'; S` [-1 - 4]. - Equilateral triangle ABC
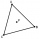 In the equilateral triangle ABC, K is the center of the AB side, the L point lies on one-third of the BC side near point C, and point M lies on one-third of the side of the AC side closer to point A. Find what part of the ABC triangle contains the triangl
In the equilateral triangle ABC, K is the center of the AB side, the L point lies on one-third of the BC side near point C, and point M lies on one-third of the side of the AC side closer to point A. Find what part of the ABC triangle contains the triangl - triangle 5420
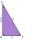 Two pairs of parallel lines, AB to CD and AC to BD, are given. Point E lies on the line BD, point F is the midpoint of the segment BD, point G is the midpoint of the segment CD, and the area of the triangle ACE is 20 cm². Determine the area of triangl
Two pairs of parallel lines, AB to CD and AC to BD, are given. Point E lies on the line BD, point F is the midpoint of the segment BD, point G is the midpoint of the segment CD, and the area of the triangle ACE is 20 cm². Determine the area of triangl - Rhombus construction
 Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides.
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides. - Katy MO
 Kate drew a triangle ABC. The middle of the line segment AB is marked as X, and the center of the side AC is marked as Y. On the side BC, she wants to find point Z so that the area of a 4gon AXZY is the greatest. What part of the ABC triangle can maximall
Kate drew a triangle ABC. The middle of the line segment AB is marked as X, and the center of the side AC is marked as Y. On the side BC, she wants to find point Z so that the area of a 4gon AXZY is the greatest. What part of the ABC triangle can maximall
