11990 perimeter RT
A right triangle has integer side lengths and a perimeter of 11990. In addition, we know that one of its perpendiculars has a prime number length. Find its length.
Final Answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a system of equations and are looking for calculator system of linear equations?
Do you solve Diofant problems and are looking for a calculator of Diofant integer equations?
See also our right triangle calculator.
Do you have a system of equations and are looking for calculator system of linear equations?
Do you solve Diofant problems and are looking for a calculator of Diofant integer equations?
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsGrade of the word problem
Related math problems and questions:
- RT with rectangle
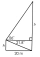 In the diagram, find the lengths h and b. One rectangle and one right triangle share one side. We know two angles and the length of the common side, as shown in the picture.
In the diagram, find the lengths h and b. One rectangle and one right triangle share one side. We know two angles and the length of the common side, as shown in the picture. - Rectangle and diagonal
 In the rectangle ABCD, we know the side length is AB = 16 cm, and the diagonal AC = 20 cm. Calculate its perimeter and area.
In the rectangle ABCD, we know the side length is AB = 16 cm, and the diagonal AC = 20 cm. Calculate its perimeter and area. - The right triangle
 In the right triangle ABC with a right angle at C, we know the side lengths AC = 9 cm and BC = 7 cm. Calculate the length of the remaining side of the triangle and the size of all angles.
In the right triangle ABC with a right angle at C, we know the side lengths AC = 9 cm and BC = 7 cm. Calculate the length of the remaining side of the triangle and the size of all angles. - Circumference of a triangle
 The circumference of the triangle is 104 cm. One side is 6 cm longer and 8 cm shorter than the third. Find the lengths of its sides.
The circumference of the triangle is 104 cm. One side is 6 cm longer and 8 cm shorter than the third. Find the lengths of its sides. - Recursion squares
 In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 20 cm. Calculate: a) the sum of peri
In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 20 cm. Calculate: a) the sum of peri - The height of prism
 A right triangle forms the base of the vertical prism with perpendiculars 30 cm and 40 cm long. This prism has the same volume as a cube with an edge length of 3 dm. Find its height in cm.
A right triangle forms the base of the vertical prism with perpendiculars 30 cm and 40 cm long. This prism has the same volume as a cube with an edge length of 3 dm. Find its height in cm. - A rectangle 2
 A rectangle has a diagonal length of 74cm. Its side lengths are in a ratio of 5:3. Find its side lengths.
A rectangle has a diagonal length of 74cm. Its side lengths are in a ratio of 5:3. Find its side lengths.
