Calculate 6539
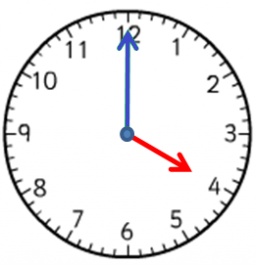
Calculate the magnitude of the angle formed by the lines p and q, which connect 1, 6 (line p), and 5, 8 (line q) on the clock face.
Correct answer:
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
You need to know the following knowledge to solve this word math problem:
- geometry
- line
- vector
- inscribed angle theorem
- arithmetic
- absolute value
- planimetrics
- circle
- basic functions
- reason
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Clock face
A clock face is drawn on paper. Straight lines connect numbers 10 and 5 and 3 and 8. Calculate the size of their angles. - Corresponding 82704
On the circular face of the clock, we connect the points corresponding to the numbers 2, 5, and 9 to each other, which creates a triangle. Calculate the sizes of all interior angles. - Corresponding 79314
On the circular face of the clock, we connect the points corresponding to the numbers 2, 9, and 11, which creates a triangle. Calculate the sizes of all the interior angles of that triangle. - Calculate 82282
Calculate the sizes of the interior angles in the triangle whose vertices are the points marked by the numbers 1, 5, and 8 on the clock face.
- Draw it!
Draw two lines c, d that c || d. On line c, mark points A and B. By point A, a lead perpendicular line to c. By point B, lead perpendicular line to c. - Intersection 3383
A regular 15-angle is given. A triangle is formed if we connect points 3 and 7, 13 and 10. The vertices are 3 and 13, and the lines' intersections are 3.7 and 13.10. We are to determine the angle size formed by sides 3.7 and 13.10. These numbers indicate - Tangents to ellipse
Find the magnitude of the angle at which the ellipse x² + 5 y² = 5 is visible from the point P[5, 1]. - ABCDEFGHIJKL 8426
The given is a regular hexagonal prism ABCDEFGHIJKL, which has all edges of the same length. Find the degree of the angle formed by the lines BK and CL in degrees. - Straight lines
Draw two lines c, d so that c || d. On line c, mark points A, and B, from point A starts perpendicular to line c, from point B perpendicular to line c.
- Calculate 82992
Given cuboid ABCDEFGH. We know that |AB| = 1 cm, |BC| = 2 cm, |AE| = 3 cm. Calculate in degrees the angle size formed by the lines BG and FH . - Internal angles
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det - Convex angle
There is a circle k (S; r), and a point A, which lies on this circle. There is also a point B on the circumference, for which it is true that in one direction, it is five times further from point A than in the opposite direction (around the circumference - Construct 8
Construct an analytical geometry problem where it is asked to find the vertices of a triangle ABC: The vertices of this triangle are points A (1,7), B (-5,1) C (5, -11). The said problem should be used the concepts of distance from a point to a line, rati - Angle between lines
Calculate the angle between these two lines: p: -8x +4y +5 =0 q: 10x +10y -7=0
- Trapezium diagonals
It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC. - Pentagon
The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm - Direction vector
The line p is given by the point P [- 0,5; 1] and the direction vector s = (1,5; - 3) determines: A) value of parameter t for points X [- 1,5; 3], Y [1; - 2] lines p B) whether the points R [0,5; - 1], S [1,5; 3] lies on the line p C) parametric equations
