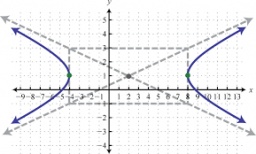
Hyperbola
Find the equation of hyperbola that passes through the point M [30; 24] and has focal points at F1 [0; 4 sqrt 6], F2 [0; -4 sqrt 6].
Result
Result
Tips for related online calculators
Looking for help with calculating arithmetic mean?
Looking for a statistical calculator?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Looking for a statistical calculator?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
statisticsgeometryplanimetricsGrade of the word problem
Related math problems and questions:
- Circle - analytics geometry
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - Hyperbola equation
Find the hyperbola equation with the center of S [0; 0], passing through the points: A [5; 3] B [8; -10] - Equation 80525
Write the equation of the parabola that passes through the points: A[1,1] B[3,-1] C[1,2] - The tangent of the hyperbola
Write the equation of the tangent of the hyperbola 9x²−4y²=36 at the point T =[t1,4]. - Circle
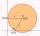Write the equation of a circle that passes through the point [0,6] and touches the X-axis point [5,0]: (x-x_S)²+(y-y_S)²=r² - Function 3
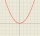Function f(x)=a(x-r)(x-s) the graph of the function has an x-intercept at (-4, 0) and (2, 0) and passes through the point (-2,-8). Find constant a, r, s. - Coordinate 82580
Write the equation of the ellipse that passes through the points, and its axes are identical to the coordinate axes when A = [2, 3] and B = [−1, −4].
