Diofant equation
250x + 120y = 5640
Correct answer:
Tips for related online calculators
Do you solve Diofant problems and are looking for a calculator of Diofant integer equations?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Well-known 5640
Students want to get from Žilina to Bratislava for a concert by a well-known music group. The distance between these places is 200 km. The estimated average speed is 80 km per hour. How long will it take them to travel? - Linsys2
Solve two equations with two unknowns: 400x+120y=147.2 350x+200y=144 - Quadratic equation
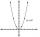Solve a quadratic equation: 2x²+28x-550=0 - Expression - decimals
Specify the value of the expression with decimal numbers: (4.416356) -7.152+ (74.855) =?
The height and radius of a cylinder are 25 ft and 5 ft, respectively. What is the surface area?
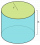Find the surface area of the cylindrical solid whose radius is 7.7 cm and height is 12 cm.
For what primes p,q,r is true: p²-(q+r)²=647