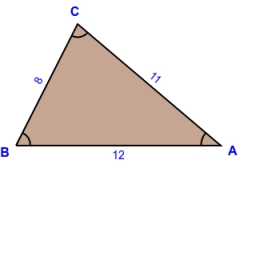
Sss triangle
Calculate the area and heights in the triangle ABC by sides a = 8cm, b = 11cm, c = 12cm
Final Answer:
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsGrade of the word problem
Related math problems and questions:
- Triangle
Calculate the triangle's heights ABC if the triangle's sides are a=26, b=81, and c=73. - Triangle and its heights
Calculate the length of the sides of the triangle ABC if va=13 cm, vb=15 cm and side b are 5 cm shorter than side a. - Right Triangle Sides Area
In the right triangle ABC, we know the right angle γ, the area S = 48 cm2, and the side a = 8 cm. Calculate: pages b, c - Parallelogram Side Heights
The parallelogram is given by: a, b is adjacent sides, va, vb - the respective heights to the individual sides. Calculate its side a, if b = 6cm, va = 3cm, vb = 4cm - Calculate triangle
In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and areas if given a=40cm, b=57cm, and c=59cm. - Triangle area percentage
A right-angled triangle ABC has sides a = 5 cm, b = 8 cm. The similar triangle A'B'C' is 2.5 times smaller. Calculate the percentage of the area of triangle ABC that is the area of triangle A'B'C'. - Circumscribed circle ABC
Triangle ABC, with sides a = 15 cm, b = 17.4 cm, and c = 21.6 cm, is circumscribed by a circle. Calculate the area of the segments determined by the sides of the triangle.
