Precious metals
From 2006-2009, the value of precious metals changed rapidly. The data in the following table represent the total rate of return (in percentage) for platinum, gold, and silver from 2006 through 2009: Year Platinum Gold Silver 2009 62.7 25.0 56.8 2008 -41.3 4.3 -26.9 2007 36.9 31.9 14.4 2006 15.9 23.2 46.1 a. Compute the geometric mean rate of return per year for platinum, gold, and silver from 2006 through 2009. b. What conclusions can you reach concerning the geometric mean rates of the three precious metals?
Your answer:
Your answer:
Showing 1 comment:
Tips for related online calculators
Looking for a statistical calculator?
Our percentage calculator will help you quickly and easily solve a variety of common percentage-related problems.
Do you want to round the number?
Our percentage calculator will help you quickly and easily solve a variety of common percentage-related problems.
Do you want to round the number?
You need to know the following knowledge to solve this word math problem:
statisticsarithmeticbasic operations and conceptsGrade of the word problem
Related math problems and questions:
- Z-score
The mean adult male pulse rate is 67.3 beats per minute, with a standard deviation of 10.3. Find the z-score for an adult male's pulse rate of 75. (Round the z-score to two decimal places. ) - N percentille problem
Here is a data set (n=117) that has been sorted. 10.4 12.2 14.3 15.3 17.1 17.8 18 18.6 19.1 19.9 19.9 20.3 20.6 20.7 20.7 21.2 21.3 22 22.1 22.3 22.8 23 23 23.1 23.5 24.1 24.1 24.4 24.5 24.8 24.9 25.4 25.4 25.5 25.7 25.9 26 26.1 26.2 26.7 26.8 27.5 27.6 2 - Standard deviation
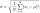Find the standard deviation for the following grouped data: Age (years); Number of Persons 0–10; 15 10–20; 15 20–30; 23 30–40; 22 40–50; 25 50–60; 10 60–70; 5 70–80; 10 - The raw
The raw data presented here are the scores (out of 100 marks) of a market survey regarding the acceptability of a new product launched by a company for a random sample of 50 respondents: 40 45 41 45 45 30 30 8 48 25 26 9 23 24 26 29 8 40 41 42 39 35 18 25 - Estimate the mode
A medium-sized asset management firm has 56 fund managers. Each of these managers has its own portfolio. The percentage returns from the managers' portfolios are shown in the table below: Return percentage; Number of managers 0-10; 8 10-20; 18 20-30; 21 3 - Airport 4
The airport in Košice collected the following data on aircraft delays within one week: (Solve the following tasks without classification into intervals. Round the results to 2 decimal places) Aircraft delay in min.: 541; 545; 575; 520; 572; 544; 524; 567; - Salami
We have six kinds of salami, six of which have ten pieces, and one of which has four pieces. How many ways can we distinctly choose five pieces of salami?
