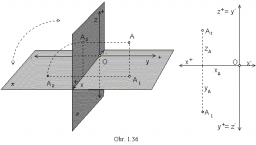
Symmetry by plane

Determine the coordinates of an image of point A (3, -4, -6) at a symmetry that is determined by the plane x-y-4z-13 = 0

Final Answer:

x =  1
y =  -2
z =  2

Step-by-step explanation:

r:x−y−4z−13=0 A(3,−4,−6)  n = s n = (1,−1,−4) p: x = t+a; y = −t+b; z = −4t + c; t ∈ R  3=t+a −4=−t+b −6=−4⋅ t+c t=1  a+t=3 b−t=−4 c−4t=−6  c=−6+4t=−6+4⋅ 1=−2 b=−4+t=−4+1=−3 a=3−t=3−1=2  a=2 b=−3 c=−2  p: x = t+2; y=−t−3; z = −4t−2; t ∈ R  p(t=−1) = A′  x=−1+a=−1+2=1
y=−(−1)+b=−(−1)+(−3)=−2
z=−4⋅ (−1)+c=−4⋅ (−1)+(−2)=2

Try another example


Did you find an error or inaccuracy? Feel free to send us. Thank you!







Tips for related online calculators
The line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.

You need to know the following knowledge to solve this word math problem:

geometryalgebrabasic operations and conceptsGrade of the word problem

Related math problems and questions: