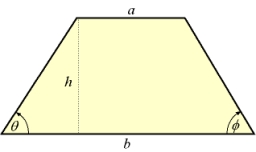
Isosceles trapezium
Calculate the area of an isosceles trapezium ABCD if a = 10cm, b = 5cm, c = 4cm.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Isosceles
Isosceles trapezium ABCD ABC = 12 angle ABC = 40 ° b=6. Calculate the circumference and area. - Internal angles IST
Determine internal angles of isosceles trapezium ABCD /a, c are the bases/ and if: alpha:gamma = 1:3 - Calculate 48073
Calculate the area of the isosceles trapezoid ABCD if a = 14 cm, c = 8 cm, and the size of the angle DAB is 52 °. - Trapezoid - intersection of diagonals
In the ABCD trapezoid is AB = 8 cm long, trapezium height 6 cm, and distance of diagonals intersection from AB is 4 cm. Calculate the trapezoid area. - Height—the 6183
In the isosceles trapezoid ABCD, the base length is a = 10cm, c = 6cm, and the arm's length is 4cm. Calculate its height—the result round to tenths. - Isosceles trapezoid
Isosceles trapezoid ABCD, AB||CD is given by |CD| = c = 12 cm, height v = 16 cm and |CAB| = 20°. Calculate area of the trapezoid. - The trapezium
The trapezium is formed by cutting the top of the right-angled isosceles triangle. The trapezium base is 10 cm, and the top is 5 cm. Find the area of the trapezium. - Parameters: 36691
Calculate the length of the arms and the area of the isosceles trapezoid if you know the following parameters: o = 20 cm a = 10 cm, c = 4 cm h = 2 cm - The bases
The bases of the isosceles trapezoid ABCD have 10 cm and 6 cm lengths. Its arms form an angle α = 50˚ with a longer base. Calculate the circumference and area of the ABCD trapezoid. - Trapezoidal base
Calculate the surface and volume of a quadrilateral prism with a trapezoidal base, where a = 7 cm, b = 4 cm, c = 5 cm, d = 4 cm, height of trapezium v = 3.7 cm and the height of the prism h = 5 cm. - Isosceles 5666
In the isosceles trapezoid ABCD, calculate the missing side length "a" and then its areas. Side b = d = 50 cm, c = 20 cm, height = 48 cm. - Calculate 2556
Calculate the arm size b of the trapezoid ABCD if a = 12 cm, c = 4 cm, d (AC) = d (BC) and the area S (triangle ABC) = 9 cm square. - Circumference 2598
Calculate the circumference and area of the parallelogram ABCD, if a = 72cm and v = 4.3cm b = 6cm - Trapezium
Find the height of the trapezium ABCD, which has area 77.5 cm² and base lengths 16 cm and 15 cm. - Isosceles 7929
ABCD isosceles trapezoid. A = 6cm, e = 7cm and delta angle = 105 °. Calculate the remaining pages. - Trapezium diagonals
It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC. - Similarity 30821
There is a given square ABCD with a = 5.3cm. Determine the side size of a similar square if the similarity ratio k = 3cm. Calculate the area and the perimeter of the magnified square
