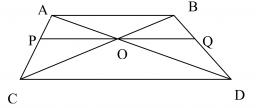
Trapezoid - intersection of diagonals
In the ABCD trapezoid is AB = 8 cm long, trapezium height 6 cm, and distance of diagonals intersection from AB is 4 cm. Calculate the trapezoid area.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Trapezium diagonals
It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC. - Diamond area from diagonals
In the diamond, ABCD is AB = 4 dm, and the diagonal length is 6.4 dm long. What is the area of the diamond? - Isosceles trapezium
Calculate the area of an isosceles trapezium ABCD if a = 10cm, b = 5cm, c = 4cm. - Diagonal intersect
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles? - Ratio in trapezium
The height v and the base a, c in the trapezoid ABCD is in the ratio 1:6:3, its area S = 324 square cm. Peak angle B = 35 degrees. Determine the perimeter of the trapezoid - Diagonals in diamons/rhombus
Rhombus ABCD has a side length AB = 4 cm and a length of one diagonal of 6.4 cm. Calculate the length of the other diagonal. - Isosceles
Isosceles trapezium ABCD ABC = 12 angle ABC = 40 ° b=6. Calculate the circumference and area. - Trapezium bases
Find the trapezium height if a = 8 cm and c = 4 cm if its area is 21 square centimeters. - Cross section
The cross-section ABCD of a swimming pool is a trapezium. Its width AB=14 meters, depth at the shallow end is 1.5 meters, and at the deep end is 8 meters. Find the area of the cross-section. - Diagonal The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm, CD = 4cm. Calculate the length of the AC diagonal.
- Diagonals at right angle
In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD? - trapezium 3428
Given is a trapezoid ABCD with bases AB, CD. Let K be side AB's midpoint, and point L be side CD's midpoint. The area of triangle ALB is 15 cm2, and the area of triangle DKC is 10 cm². Calculate the area of trapezium ABCD. - Rectangular trapezoid
The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters - A kite
ABCD is a kite. Angle OBC = 20° and angle OCD = 35°. O is the intersection of diagonals. Find angle ABC, angle ADC and angle BAD. - One trapezium
One trapezium has AB=24M, BC=36M, CD=80M, DA=80M long sides. Find the area. - Trapezoidal base
Calculate the surface and volume of a quadrilateral prism with a trapezoidal base, where a = 7 cm, b = 4 cm, c = 5 cm, d = 4 cm, height of trapezium v = 3.7 cm and the height of the prism h = 5 cm. - Swimming pool
A swimming pool 30 meters long is filled with water to a depth of 1 meter at the shallow end, and 5 meters at the deep end, and abcd the vertical area of the pool has the shape of a trapezium with the area given by S(abcd)= 1/2 (ab + cd) x ad. What is the
