Pythagorean theorem - practice problems - page 6 of 73
Number of problems found: 1451
- Height UT
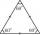How long is the height in the equilateral triangle with a side f = 31? - Binomials
To binomial 100x²-260x, add a number to the resulting trinomial be square of the binomial. - Equilateral triangle Calculate the side of an equilateral triangle if its area is 886 mm².
- Circle
The circle k with diameter |MN| = 85. Point J lies on the circle k. Line |NJ|=12. Calculate the length of a segment JM. - Iso triangle
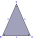An isosceles triangle with a base of 8 cm. Its circumference is 28 cm. Calculate the height of the triangle. - Calculate 7762
Calculate the size of the diagonal of an ABCD square whose perimeter is 40cm - Rhombus 47
A rhombus has a side length of 5 m and a longer diagonal length of 8 m. What is the length of the shorter diagonal of the rhombus? - The diagonals
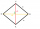The diagonals in the diamond ABCD are 6 cm and 8 cm long. What is the perimeter of this diamond? - The triangle
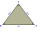The triangle has sides 5 cm long, 5 cm, and 8 cm long. What is the area of the triangle? - ABC isosceles
ABC isosceles rights triangle the length of each leg is 1 unit what is the length of the hypotenuse AB in the exact form - Right isosceles triangle
What can be the area of a right isosceles triangle with a side length of 8 cm? - Diagonal to area
Calculate the area of a rectangle in which the diagonal length is 10 cm. - Equilateral triangle
The equilateral triangle has a 23 cm long side. Calculate its area. - Calculate chord
A circle k (S, 5cm) is given. Calculate the length of the chord of the circle k if it is 3 cm from the center S. - Rhombus
Find the length of the other diagonal and the area of the rhombus. The perimeter of a rhombus is 56 cm, and one of the diagonals is of length 14 cm. - Right triangle
Right triangle ABC with side a = 10 and the area S = 50. Calculate the length of the remaining sides. - Circumscription
Calculate the radius of the Circumscribed circle in the rectangle with sides 3 and 6. Can it be a rectangle inscribed by a circle? - Square and circles
Square with sides 68 km is circumscribed and inscribed with circles. Determine the radiuses of both circles. - Surrounded 36661
Calculate the length of the circle, which is surrounded by a square with a side length of 3 cm - Calculate 6198
Calculate the diagonal length of the 87 cm and 60 cm TVs and round the result to units.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
