Absolute value - practice problems - page 4 of 8
Remember: Solve each problem thoughtfully and make sure to show your complete solution for every question.Number of problems found: 142
- The modulus
Find the modulus of the complex number 2 + 5i - Trapezoid perimeter calculation
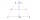Find the points A1 B1 symmetric along the y-axis to the points A [-4,0] and B [-1,4]. Calculate the perimeter of the trapezoid AB B1 A1. - Angle of the body diagonals
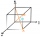Using the vector dot product calculate the angle of the body diagonals of the cube. - Suppose
Suppose you know that the length of a line segment is 15, x2=6, y2=14, and x1= -3. Find the possible value of y1. Is there more than one possible answer? Why or why not? - Two chords
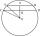Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords. - Clock hand angle
What is the angle of the clock hands: a / at 16 hours 15 minutes b / v 8 hours and 4 minutes - Absolute value inequality
Solve on Z - inequality with absolute value: | x-18 | +4> 1 - Absolute reciprocal calculation What do I get by multiplying the absolute value of -0.7 and the reciprocal number of 10? What do I get by dividing the opposite number by the number -14/8 and the reciprocal number to the number 4?
- Magic number conjuring
Roman likes magic and math. Last time he conjured three- or four-digit numbers like this: • created two new numbers from the given number by dividing it between digits in the place of hundreds and tens (e.g., from the number 581, he would get 5 and 81), • - Sloth meeting distance
There are two sloths in the tree's branches. One is 2.5 m from the trunk, and the other is on the other side of the tree, 4 m from the trunk. The sloths head out to get to know each other. Calculate how far from the log they will meet if they climb at the - Temperature difference 2
The temperature in London on New Year's Day is -2 degrees Celsius. The temperature in Prague on the same day is -14 degrees Celsius. What is the temperature difference between the two cities? - Distance Between Boats
An observer watches two boats at depth angles of 64° and 48° from the top of the hill, which is 75 m above the lake level. Determine the distance between the boats if both boats and the observer are in the same vertical plane. - Lighthouse
Marcel (point J) lies in the grass and sees the top of the tent (point T) and, behind it, the top of the lighthouse (P). | TT '| = 1.2m, | PP '| = 36m, | JT '| = 5m. Marcel lies 15 meters away from the sea (M). Calculate the lighthouse distance from the s - Cube root
For 13, Sam wrote 2891 instead of the correct cube number. By how much was he wrong? - Coordinates of square vertices
The ABCD square has the center S [−3, −2] and the vertex A [1, −3]. Find the coordinates of the other vertices of the square. - Clock Hands Angle Ten
The hour and minute hands on the clock face make an alpha angle. If you know it's 10 hours and 12 minutes, what is the angle's size? - Middle number puzzle
In the middle between the unknown number and the number 166 is the number a) 164, b) 200, c) 500 d) 1356 What are the unknown numbers? - Number axis distance How many double-digit numbers lie on the number axis closer to the number 31 than to the number 100?
- Vertices of a right triangle
Show that the points D(2,1), E(4,0), and F(5,7) are vertices of a right triangle. - Three points
Three points: A (-3;-5), B (9;-10), and C (2;k). AB=AC What is the value of k?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
