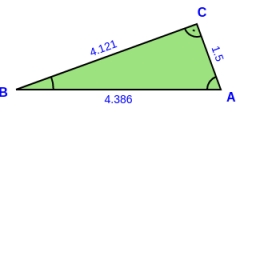
Vertices of a right triangle
Show that the points D(2,1), E(4,0), and F(5,7) are vertices of a right triangle.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryarithmeticplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Vertices of RT
Show that the points P1 (5,0), P2 (2,1) & P3 (4,7) are the vertices of a right triangle. - Points collinear
Show that the point A(-1,3), B(3,2), C(11,0) are col-linear. - Quadrilateral 2
Show that the quadrilateral with vertices A(0,1), B(4,2), C(3,6) D(-5,4) has two right triangles. - Construct 8
Construct an analytical geometry problem where it is asked to find the vertices of a triangle ABC: The vertices of this triangle are points A (1,7), B (-5,1) C (5, -11). The said problem should be used the concepts of distance from a point to a line, rati
- Determine 82341
Determine the equation of the circle that is the set of all points of the plane that are twice as far from the point [3,7] as they are from the point [0,1]. - Curve and line
The equation of a curve C is y=2x² -8x+9, and the equation of a line L is x+ y=3 (1) Find the x coordinates of the points of intersection of L and C. (2) Show that one of these points is also the stationary point of C? - Three points 2
The three points are A(3, 8), B(6, 2), and C(10, 2). Point D is such that the line DA is perpendicular to AB, and DC is parallel to AB. Calculate the coordinates of D.
