Quadrilateral 2
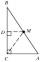
Show that the quadrilateral with vertices A(0,1), B(4,2), C(3,6) D(-5,4) has two right triangles.
Final Answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryarithmeticplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Vertices of RT
 Show that the points P1 (5,0), P2 (2,1) & P3 (4,7) are the vertices of a right triangle.
Show that the points P1 (5,0), P2 (2,1) & P3 (4,7) are the vertices of a right triangle. - Vertices of a right triangle
 Show that the points D(2,1), E(4,0), and F(5,7) are vertices of a right triangle.
Show that the points D(2,1), E(4,0), and F(5,7) are vertices of a right triangle. - Points collinear
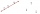 Show that the point A(-1,3), B(3,2), C(11,0) are col-linear.
Show that the point A(-1,3), B(3,2), C(11,0) are col-linear. - What is 10
 What is The area of a parallelogram that has vertices with the coordinates (0, 0), (4, 0),(5, 3), and (1, 3)?
What is The area of a parallelogram that has vertices with the coordinates (0, 0), (4, 0),(5, 3), and (1, 3)? - Hyperbola
 Find the equation of hyperbola that passes through the point M [30; 24] and has focal points at F1 [0; 4 sqrt 6], F2 [0; -4 sqrt 6].
Find the equation of hyperbola that passes through the point M [30; 24] and has focal points at F1 [0; 4 sqrt 6], F2 [0; -4 sqrt 6]. - The plaster cast
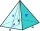 The plaster cast has the shape of a regular quadrilateral pyramid. The cover consists of four equilateral triangles with a 5 m side. Calculate its volume and surface area.
The plaster cast has the shape of a regular quadrilateral pyramid. The cover consists of four equilateral triangles with a 5 m side. Calculate its volume and surface area. - Field with vegetables
 The field planted with vegetables has a rectangular isosceles triangle with a leg length of 24 m. At the triangle's vertices are rotating sprinklers with a range of 12 m. How much of the field sprinkler isn't irrigated?
The field planted with vegetables has a rectangular isosceles triangle with a leg length of 24 m. At the triangle's vertices are rotating sprinklers with a range of 12 m. How much of the field sprinkler isn't irrigated?
