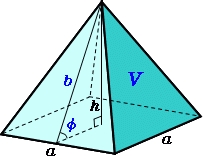
The plaster cast
The plaster cast has the shape of a regular quadrilateral pyramid. The cover consists of four equilateral triangles with a 5 m side. Calculate its volume and surface area.
Your answer:
Your answer:
Tips for related online calculators
See also our right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetryGrade of the word problem
Related math problems and questions:
- The cast
The cast in the body of a regular quadrilateral pyramid with a base edge 60 cm long and 5 cm high is made of a material with a density of 7.8 g/cm cubic. Calculate its weight. - Quadrangular pyramid
Given is a regular quadrilateral pyramid with a square base. The body height is 30 cm, and volume V = 1000 cm³. Calculate its side and its surface area. - Quadrangular pyramid
The regular quadrilateral pyramid has a base length of 6 cm and a side edge length of 9 centimeters. Calculate its volume and surface area. - Pyramid Height Surface Area
The regular quadrilateral pyramid has a base diagonal of 5√2 cm, and the side edges are 12√2 cm long. Calculate the height of the pyramid and its surface. - Pyramid surface
There is a regular quadrilateral pyramid with the base edge length a = 3 cm and with the length of the side edge h = 8 cm. Please calculate its surface area and volume. - Quadrilateral pyramid
The regular quadrilateral pyramid has a base perimeter of 44 cm and a body height of 3.2 cm. Calculate its volume and surface. - The regular
The regular quadrilateral pyramid has a volume of 24 dm³ and a height of 45 cm. Calculate its surface.
