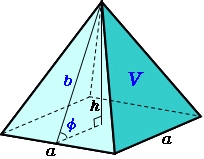
Quadrangular pyramid

The regular quadrangular pyramid has a base length of 6 cm and a side edge length of 9 centimeters. Calculate its volume and surface area.

Correct answer:

V =  95.247 cm³
S =  137.8234 cm²

Step-by-step explanation:

$$\begin{gathered} a=6\text{ cm } \\ s=9\text{ cm } \\ {S}_1=a^2=6^2=36{\text{cm}}^2 \\ u=\sqrt{2}\cdot a=\sqrt{2}\cdot 6=6\sqrt{2}\text{ cm}\doteq 8.4853\text{ cm } \\ h=\sqrt{s^2-(u\mathrm{/}2{)}^2}=\sqrt{9^2-(8.4853\mathrm{/}2{)}^2}=3\sqrt{7}\text{ cm}\doteq 7.9373\text{ cm } \\ V={\displaystyle \frac{1}{3}}\cdot S_1\cdot h={\displaystyle \frac{1}{3}}\cdot 36\cdot 7.9373=36\sqrt{7}=95.247{\text{cm}}^3 \end{gathered}$$

$$\begin{gathered} h_2=\sqrt{s^2-(a\mathrm{/}2{)}^2}=\sqrt{9^2-(6\mathrm{/}2{)}^2}=6\sqrt{2}\text{ cm}\doteq 8.4853\text{ cm } \\ {S}_2=a\cdot h_2\mathrm{/}2=6\cdot 8.4853\mathrm{/}2=18\sqrt{2}{\text{cm}}^2\doteq 25.4558{\text{cm}}^2 \\ S=S_1+4\cdot S_2=36+4\cdot 25.4558=137.8234{\text{cm}}^2 \end{gathered}$$

Try another example

Related math problems and questions:

• Tetrahedral pyramid
  A regular tetrahedral pyramid is given. Base edge length a = 6.5 cm, side edge s = 7.5 cm. Calculate the volume and the area of its face (side area).
• Quadrangular pyramid
  Given is a regular quadrangular pyramid with a square base. The body height is 30 cm and volume V = 1000 cm³. Calculate its side a and its surface area.
• Regular quadrilateral pyramid
  What is the volume of a regular quadrilateral pyramid if its surface is 576 cm² and the base edge is 16 cm?
• Tetrahedral pyramid
  It is given a regular tetrahedral pyramid with base edge 6 cm and the height of the pyramid 10 cm. Calculate the length of its side edges.
• Quadrangular pyramid
  Calculate the surface area and volume of a regular quadrangular pyramid: sides of bases (bottom, top): a1 = 18 cm, a2 = 6cm angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.) S =? , V =?
• Quadrilateral pyramid
  Calculate the surface of a quadrilateral pyramid, which has a rectangular base with dimensions a = 8 cm, b = 6 cm and height H = 10 cm.
• Pyramid
  The pyramid has a base rectangle with a = 6cm, b = 8cm. The side edges are the same and their length = 12.5 cm. Calculate the surface of the pyramid.
• Pyramid 8
  Calculate the volume and the surface area of a regular quadrangular pyramid with the base side 9 cm and side wall with the base has an angle 75°.
• Regular quadrilateral pyramid
  Find the volume and surface of a regular quadrilateral pyramid if the bottom edge is 45 cm long and the pyramid height is 7 cm.
• Quadrilateral pyramid
  We have a regular quadrilateral pyramid with a base edge a = 10 cm and a height v = 7 cm. Calculate 1/base content 2/casing content 3/pyramid surface 4/volume of the pyramid
• Quadrangular prism
  Calculate the volume and surface area of a regular quadrangular prism 35 cm high and the base diagonal of 22 cm.
• Quadrilateral pyramid,
  A quadrilateral pyramid, which has a rectangular base with dimensions of 24 cm, 13 cm. The height of the pyramid is 18cm. Calculate 1/the area of the base 2/casing area 3/pyramid surface 4/volume of the pyramid
• Pyramid 4sides
  Calculate the volume and the surface of a regular quadrangular pyramid when the edge of the base is 4 cm long and the height of the pyramid is 7 cm.
• Truncated pyramid
  Find the volume and surface area of a regular quadrilateral truncated pyramid if base lengths a1 = 17 cm, a2 = 5 cm, height v = 8 cm.
• Wall height
  Calculate the surface and volume of a regular quadrangular pyramid if side a = 6 cm and wall height v = 0.8dm.
• Quadrangular prism
  The regular quadrangular prism has a base edge a = 7.1 cm and side edge = 18.2 cm long. Calculate its volume and surface area.
• Hexagon cut pyramid
  Calculate the volume of a regular 6-sided cut pyramid if the bottom edge is 30 cm, the top edge is 12 cm, and the side edge length is 41 cm.