Pravidelný 4
Pravidelný štvorboký ihlan má dĺžku podstavnej hrany 6 cm a dĺžka bočnej hrany je 9 centimetrov. Vypočítaj objem a obsah
Správna odpoveď:
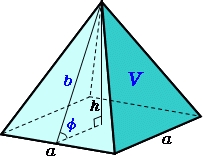
Tipy na súvisiace online kalkulačky
Chcete premeniť jednotku dĺžky?
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- vyjadrenie neznámej zo vzorca
- stereometria
- ihlan
- povrch telesa
- planimetria
- Pytagorova veta
- pravouhlý trojuholník
- trojuholník
- štvoruholník
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Pravidelný 18
Pravidelný štvorboký ihlan má objem 2 160 litrov a dĺžku podstavnej hrany 12dm. Vypočítaj výšku ihlana (náčrt, výpočet, odpoveď). - Štvorboký hranol
Vypočítaj objem pravidelného štvorbokého ihlana, ktorý má veľkosť podstavnej hrany a = 8 cm a veľkosť bočnej hrany h = 9 cm. - Vypočítajte 5130
Je daný pravidelný štvorboký ihlan s dĺžkou podstavnej hrany a = 3 cm as dĺžkou bočnej hrany h = 8 cm. Vypočítajte prosím jeho povrch a objem. - Ihlan
Je daný pravidelný štvorboký ihlan, dĺžka podstavné hrany je 6 cm a výška ihlanu je 10 cm. vypočítajte dĺžku bočnej hrany.
- Pravidelný 46641
Pravidelný trojboký ihlan ABCDV má dĺžku podstavnej hrany a = 8 cm a výšku 7 cm. Vypočítaj povrch a objem ihlana - Vypočítajte 44471
Pravidelný štvorboký ihlan má povrch 260 cm² a obsah jednej bočnej steny 40 cm². Vypočítajte dĺžku hrany podstavy a stenovú výšku. - Pravidelný 4bi
Pravidelný štvorboký ihlan má uhlopriečku podstavy 5√2 cm a bočné hrany majú dĺžku 12√2 cm. Vypočítaj výšku ihlana a jeho povrch.
