Vrcholy trojuholníka
Ukážte, že body D (2,1), E (4,0), F (5,7) sú vrcholy pravouhlého trojuholníka.
Správna odpoveď:
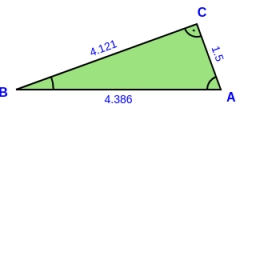
Tipy na súvisiace online kalkulačky
Chcete premeniť jednotku dĺžky?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
geometriaaritmetikaplanimetriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Body - vrcholy
Ukážte, že body P1 (5,0), P2 (2,1) a P3 (4,7) sú vrcholy pravého trojuholníka. - Kolineárne body
Ukážte, že body A (-1,3), B (3,2), C (11,0) sú kolineárne (ležia na jednej priamke). - V obdĺžniku 2
V obdĺžniku so stranami dĺžok 4cm a 8cm ležia dve rôzne polkružnice, z ktorých každá má krajné body v jeho susedných vrcholoch a dotýka sa protiľahlej strany. Zostrojte štvorec taký, že jeho dva vrcholy ležia na jednej polkružnici, zvyšné dva na druhej a - Ťažnica
Vrcholy trojuholníka sú A (-1,3), B (1,-1) a C (5, 1). Nájdite dĺžku ťažnice z vrcholu C. - Súradnice vrcholov
Trojuholník PQR má vrcholy umiestnené na súradniciach (2, 2), (5, -4) a (-4, -1). Aký typ trojuholníka je trojuholník PQR? - Trojuholníka 13581
Vrcholy trojuholníka ABC ležia na kružnici tak, že ju delia na tri diely v pomere 1:2:3. Zostroj tento trojuholník. - Vpísaný trojuholník
Do kružnice je vpísaný trojuholník tak, že jeho vrcholy delia kružnicu na 3 oblúky. Dĺžky oblúkov sú v pomere 2:3:7. Urči vnútorné uhly trojuholníka.
