Square
Points A[9,9] and B[-4,1] are adjacent vertices of the square ABCD. Calculate the area of the square ABCD.
Final Answer:
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryarithmeticplanimetricsnumbersUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Square 2
Points D[10,-8] and B[1,-10] are opposed vertices of the square ABCD. Calculate the area of the square ABCD. - Calculate 7
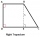Calculate the height of the trapezoid ABCD, where the coordinates of vertices are: A[2, 1], B[8, 5], C[5, 5] and D[2, 3] - Calculate 6
Calculate the distance of point A[0, 2] from a line passing through points B[9, 5] and C[1, -1]. - Point collinear coordinates
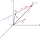Given are points A [1;a2;a3], B [3;-4;-1], C [-3;-1;8]. Points A, B, and C lie in a straight line. Calculate the coordinates a2, a3 - Square point distance
I was given a square ABCD 4.2 cm. Find the set of all points that have a distance less than or equal to 2 cm from one of its vertices and lie inside this square. Indicate how much of the square this area occupies as a percentage. - Square coordinates
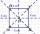The rectangular coordinate system has a point A [-2; -4] and a point S [0; -2]. Determine the coordinates of points B, C, and D so that ABCD is a square and S is the intersection of their diagonals. - Coordinates of square vertices
The ABCD square has the center S [−3, −2] and the vertex A [1, −3]. Find the coordinates of the other vertices of the square.
