Area of Polygon Problems - page 4 of 6
Number of problems found: 112
- Calculate 6566
Calculate the surface area and volume of a regular hexagonal pyramid whose base edge is 10 cm long and the side edge is 26 cm long. - Calculate 6331 The regular hexagonal pyramid has a base edge of 20 cm and a side edge of 40 cm. Calculate the height and surface of the pyramid
- Corresponding 6021
How much paint do we need to paint a pool in the shape of a 6-sided prism? The base edge measures 21 dm, the corresponding height is 1.8 m, and the pool height is 150 cm. We need 0.21 kg of paint per 1 m². - Hexagonal pyramid
The pyramid's base is a regular hexagon, which can be circumscribed in a circle with a radius of 1 meter. Calculate the volume of a pyramid 2.5 meters high. - Tower
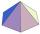The top of the tower is a regular hexagonal pyramid with a base edge 5.7 meters long and a height 7 meters. How many m² of the sheet is required to cover the top of the tower? We must add 4% of metal for waste. - Glass
How many glasses are needed to produce glass with a base of a regular 5-gon if one base triangle in the base is 4.2 square cm and the height is 10 cm? - Hexagonal pyramid
Calculate the surface area of a regular hexagonal pyramid with a base inscribed in a circle with a radius of 8 cm and a height of 20 cm. - Hexagon cut pyramid
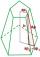Calculate the volume of a regular 6-sided cut pyramid if the bottom edge is 30 cm, the top edge is 12 cm, and the side edge length is 41 cm. - Perpendicular 79804
A perpendicular hexagonal prism was created by machining a cube with an edge length of 8 cm. The base of the prism is created from the square wall of the original cube by separating 4 identical right triangles with overhangs of lengths 3cm and 4cm. The he - Decimeters 2551
The cardboard packaging without a lid has the shape of a regular hexagonal prism with a main edge that is 12 cm long and 15 cm high. How much cardboard is used to make five packages if 10% of the cardboard is added for folds? Give results in square decime - 9-sided pyramid
Calculate the surface area and volume of a regular nine-sided pyramid if the radius of the circle inscribed in the base measures ρ = 12 cm and the height of the pyramid is 24 cm - Octagonal tank
The tank has the shape of a regular octagonal prism without an upper base. The base edge has a = 3m, and the side edge b = 6m. How much metal sheet is needed to build the tank? Do not think about losses or sheet thickness. - Tetrahedron 83144
A container shaped like a rotating cylinder with a base radius of 5 cm is filled with water. If a regular tetrahedron with an edge of 7 cm is immersed in it, how much will the water level in the container rise? - 9-gon pyramid
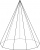Calculate a nine-sided pyramid's volume and surface, the base of which can be inscribed with a circle with radius ρ = 7.2 cm and whose side edge s = 10.9 cm. - Hexagonal pyramid
Find the volume of a regular hexagonal pyramid, the base edge 12 cm long and the side edge 20 cm. - Hexagon
Calculate the surface area of the regular hexagonal prism, whose base edge a = 12cm and side edge b = 3 dm. - The rod The rod has the shape of a regular hexagonal prism with a volume of 32.4 cubic decimetres. What is the area of the base if it is 350 centimeters long? Round to ones.
- Triangular 24091
A regular triangular prism with a base edge of 35 cm has a volume of 22.28 l. Calculate its height. - 4side pyramid
Calculate the volume and surface of the regular four-sided pyramid whose base edge is 4 cm long. The angle from the plane of the sidewall and base plane is 60 degrees. - Octagonal prism vase
We can pour 0.7 l of water into an octagonal prism vase. The vase has the bottom has an area of 25 cm square and a thickness of 12 mm. What is the height of the vase?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
