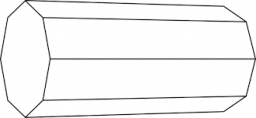
Octagonal tank
The tank has the shape of a regular octagonal prism without an upper base. The base edge has a = 3m, and the side edge b = 6m. How much metal sheet is needed to build the tank? Do not think about losses or sheet thickness.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- surface area
- prism
- planimetrics
- Pythagorean theorem
- right triangle
- polygon
- area of a shape
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Consumption 17823
The roof is a regular hexagonal pyramid shell with a wall height of v = 5 m and a base edge of a = 4 m. Calculate the consumption of sheet metal to cover the roof, assuming 15% losses. - Measuring 6159
We have a cube measuring side a = 540mm. However, it is made of 25 mm thick sheet metal. How much do I need to sheet the cubes inside and the bottom? The lid is not required. - Wooden container
The locksmith should cover the cube-shaped wooden container with a metal sheet inside. The outer edge of the container is 54cm. The wall thickness is 25 mm. The container has no lid. Calculate. How many sheets will be needed to cover it? - Diameter 30533
The open tank has the shape of a cylinder with a diameter of d = 1 m and a height of v = 2 m. How many m² of sheet metal is needed to make the tank? How many liters of water will fit in this tank?
- Four-sided 7833
The tower has the shape of a regular four-sided pyramid with a base edge of 0.8 m. The height of the tower is 1.2 meters. How many square meters of sheet metal is needed for coverage if we count eight percent for joints and overlap? - Four-sided 15613
The turret has the shape of a regular four-sided pyramid with a base edge 0.8 m long. The height of the turret is 1.2 m. How many square meters are needed to cover it, counting the extra 10% sheet metal waste? - Block-shaped 8378
How much paint does Peter use to paint a block-shaped sheet metal garage (without the lower base) with dimensions of 8m, 5.5m, and a height of 2.5m, if 1kg of paint is enough for a 4m square area?
