Basic operations and concepts - math word problems - page 298 of 322
Number of problems found: 6438
- Effectiveness 80811
 According to clinical studies, the effectiveness of the drug is 90%. The doctor prescribed the medicine to eight patients. What is the probability that the drug will be effective in all these patients?
According to clinical studies, the effectiveness of the drug is 90%. The doctor prescribed the medicine to eight patients. What is the probability that the drug will be effective in all these patients? - Four-sided 7910
 The roof of the recreation cottage has the shape of a regular four-sided pyramid with a height of 8m and a base edge of 4m. How much ℅ went to folds and joints, and 75.9 square meters of sheet metal were used to cover the roof?
The roof of the recreation cottage has the shape of a regular four-sided pyramid with a height of 8m and a base edge of 4m. How much ℅ went to folds and joints, and 75.9 square meters of sheet metal were used to cover the roof? - Insert 7
 Insert five harmonic means between 3 and 18
Insert five harmonic means between 3 and 18 - Martians
 A sphere-shaped spaceship with a diameter of 6 m landed in the meadow. To avoid attracting attention, the Martians covered it with a roof in the shape of a regular cone. How high will this roof be so that the consumption of roofing is minimal?
A sphere-shaped spaceship with a diameter of 6 m landed in the meadow. To avoid attracting attention, the Martians covered it with a roof in the shape of a regular cone. How high will this roof be so that the consumption of roofing is minimal? - Rectangle 7768
 The base of a cuboid is a rectangle. The ratio of its length to width is 3:2. The length of the rectangle of the base is in the ratio of 4:5 to the height of the block. The sum of the lengths of all the edges of the block is 2.8m. Find: a) the surface of
The base of a cuboid is a rectangle. The ratio of its length to width is 3:2. The length of the rectangle of the base is in the ratio of 4:5 to the height of the block. The sum of the lengths of all the edges of the block is 2.8m. Find: a) the surface of - Six-sided parasol
 The parasol has the shape of the shell of a regular six-sided pyramid, whose base edge is a=6dm and height v=25cm. How much fabric is needed to make a parasol if we count 10% for joints and waste?
The parasol has the shape of the shell of a regular six-sided pyramid, whose base edge is a=6dm and height v=25cm. How much fabric is needed to make a parasol if we count 10% for joints and waste? - Leveling
 Calculate how many we must purchase 25 kg bags of leveling concrete if we level room 19 m² to the "height" 11 mm if consumption is 1.7 kg per square meter and millimeter thickness.
Calculate how many we must purchase 25 kg bags of leveling concrete if we level room 19 m² to the "height" 11 mm if consumption is 1.7 kg per square meter and millimeter thickness. - How many
 How many m² of copper sheet is needed to replace the roof of a conical tower with a diameter of 13 meters and a height of 24 meters if we count 8% of the material for bending and waste?
How many m² of copper sheet is needed to replace the roof of a conical tower with a diameter of 13 meters and a height of 24 meters if we count 8% of the material for bending and waste? - The observatory
 The dome of the hemisphere-shaped observatory is 5.4 meters high. How many square meters of sheet metal need to be covered to cover it, and must we add 15 percent to the minimum amount due to joints and waste?
The dome of the hemisphere-shaped observatory is 5.4 meters high. How many square meters of sheet metal need to be covered to cover it, and must we add 15 percent to the minimum amount due to joints and waste? - The body
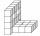 The body on the figure consists of cubes with an edge length of 7 cm. What surface has this body?
The body on the figure consists of cubes with an edge length of 7 cm. What surface has this body? - Cylindrical 6636
 A cylindrical container with a bottom diameter of 30 cm and a height of 20 cm is filled with water. We want to pour the water into another cylindrical container with a bottom diameter of 15 cm. What minimum height must the second container have for the wa
A cylindrical container with a bottom diameter of 30 cm and a height of 20 cm is filled with water. We want to pour the water into another cylindrical container with a bottom diameter of 15 cm. What minimum height must the second container have for the wa - Cylindrical 30331
 Calculate the area of sheet metal needed to make a closed cylindrical vessel with a radius of 2.5 m and a height of 1.2 m if the joints and waste count for 6%.
Calculate the area of sheet metal needed to make a closed cylindrical vessel with a radius of 2.5 m and a height of 1.2 m if the joints and waste count for 6%. - Four-sided turret
 The turret has the shape of a regular four-sided pyramid with a base edge 0.8 m long. The height of the turret is 1.2 m. How many square meters are needed to cover it, counting the extra 10% sheet metal waste?
The turret has the shape of a regular four-sided pyramid with a base edge 0.8 m long. The height of the turret is 1.2 m. How many square meters are needed to cover it, counting the extra 10% sheet metal waste? - Pyramid-shaped roof
 A block-shaped shed is covered with a quadrilateral pyramid-shaped roof with a base with sides of 6m and 3m and a height of 2.5m. How many m² (square meters) must be purchased if an extra 40% is calculated for roofing and waste?
A block-shaped shed is covered with a quadrilateral pyramid-shaped roof with a base with sides of 6m and 3m and a height of 2.5m. How many m² (square meters) must be purchased if an extra 40% is calculated for roofing and waste? - Wiring
 The conduit has a cross-section 54² mm. Maybe put it into 6 conductors with a cross section S2 $mm²?
The conduit has a cross-section 54² mm. Maybe put it into 6 conductors with a cross section S2 $mm²? - Suppose 4
 Suppose that 14% of all steel shafts produced by a certain process are nonconforming but can be reworked (rather than having to be scrapped). Consider a random sample of 200 shafts, and let X denote the number among these that are nonconforming and can be
Suppose that 14% of all steel shafts produced by a certain process are nonconforming but can be reworked (rather than having to be scrapped). Consider a random sample of 200 shafts, and let X denote the number among these that are nonconforming and can be - Water 63
 Boiler heated water at the rate of 6°c per minute for 14 minutes. It then cooled at the rate of 8°c per minute. What would be its temperature after 24 minutes if its original temperature was 40°c?
Boiler heated water at the rate of 6°c per minute for 14 minutes. It then cooled at the rate of 8°c per minute. What would be its temperature after 24 minutes if its original temperature was 40°c? - Store - silo
 A cylindrical silo (d = 4 m, h = 8 m) is about 70% full. How many m³ of silage are stored in it? Round the result to a whole number.
A cylindrical silo (d = 4 m, h = 8 m) is about 70% full. How many m³ of silage are stored in it? Round the result to a whole number. - Tin sheet
 How much sheet metal is needed for a triangular prism-shaped box with an edge of 20 cm and a height of 30 cm, the height of the base is 15 cm. An additional 10% of sheet metal is needed for gluing.
How much sheet metal is needed for a triangular prism-shaped box with an edge of 20 cm and a height of 30 cm, the height of the base is 15 cm. An additional 10% of sheet metal is needed for gluing. - Cube wall
 The surface of the first cube wall is 64 m². The second cube area is 40% of the surface of the first cube. Find the length of the edge of the second cube (x).
The surface of the first cube wall is 64 m². The second cube area is 40% of the surface of the first cube. Find the length of the edge of the second cube (x).
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
