Basic operations and concepts - math word problems - page 318 of 323
Number of problems found: 6445
- Triangulation - 3 places
Determine the distance between two inaccessible places K, L, if the angles KAL=62°10", LAB=41°23", KBL=66°34", and LBA were measured from points A, B, which are 870 m apart = 34°52". Thank you. - Cone roof consumption
The tower's roof has the shape of the shell of a rotating cone with a base diameter of 4.3 m. The deviation of the side from the plane of the base is 36°. Calculate the consumption of sheet metal to cover the roof, assuming 8% for waste. - Airship
An airship is at a height x above the ground. Pavel watches it from point A at an elevation angle of 18 degrees 26 minutes. At the same time, Peter sees it from a small plane that is currently flying over Pavel at an altitude of 150m. Peter sees the airsh - Rectangle and squares
A 9cm × 15cm rectangle is divided into unit squares. How many paths are there from one rectangle vertex to the opposite vertex if one can only go to the right and up the sides of the squares? - Octahedron - sum
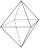On each wall of a regular octahedron is written one of the numbers 1, 2, 3, 4, 5, 6, 7, and 8, wherein on different sides are different numbers. John makes the sum of the numbers written on three adjacent walls for each wall. Thus got eight sums, which al - Slope of track
Calculate the average slope (in permille and even in degrees) of the rail tracks between Prievidza (309 m AMSL) and Horná štubňa (624 m AMSL) if the track is 37 km long. - Mast
The mast has 16 a long shadow on a slope rising from the mast foot in the direction of the shadow angle at angle 9.7°. Determine the height of the mast if the sun above the horizon is at an angle 40°48'. - Road gradient angle
On the traffic sign that informs about the road's gradient, the figure is 6.7%. Determine the slope angle of the path. What height difference is covered by the car that traveled 2.8 km on this road? - Regular octagon pad
You need to make a pad in the shape of a regular octagon with a side length of 4 cm. What is the minimum diameter of the circle-shaped semi-finished product from which we make the pad, and what will be the percentage of waste? (Round the results to 1 deci - Equilateral cylinder
A sphere is inserted into the rotating equilateral cylinder (touching the bases and the shell). Prove that the cylinder has both a volume and a surface half larger than an inscribed sphere. - Quadrilateral triangle segment
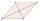The quadrilateral ABCD is symmetrical about the diagonal AC. The length of AC is 12 cm, the length of BC is 6 cm, and the interior angle at vertex B is right. points E and F are given on the sides AB, and AD so that the triangle ECF is equilateral. Determ - Cube Cut Surface Increase
We cut the cube with two mutually perpendicular cuts, each parallel to one of the cube's walls. By what percentage is the sum of the surfaces of all cuboids created in this way greater than the surface of the original cube? - Graduation of the track The gradient of the track is 9 per mile, and the distance per kilometer (on the slope) [AC] = is 560m. Determine the angle alpha and the distance [AB] = the height between A and B. A / | B/____________C
- A drone
A flying drone aimed the area for an architect. He took off perpendicularly from point C to point D. He was 300 m above ABC's plane. The drone from point D pointed at a BDC angle of 43°. Calculate the distance between points C and B in meters. - Circular railway
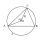The railway connects points A, B, and C in a circular arc, whose distances are | AB | = 30 km, AC = 95 km, and BC | = 70 km. How long will the track be from A to C? - Powerplant chimney
From the building window at the height of 7.5 m, we can see the top of the factory chimney at an altitude angle of 76° 30 ′. We can see the chimney base from the same place at a 5° 50 ′ depth angle. How tall is the chimney? - Square Lounge Drunken Shopper
After a long dinner, inside a lounge in the shape of a square ABCD, a drunken shopper E lies in such a way that the triangle DEC is equilateral. Spy F lies on the edge of BC, with |EB|=|EF|. What is the size of the angle CEF? - Difference - altitude
The distance as the crow flies between Dolní and Horní Ves is 3 km, and the steady climb is 5%. What is the height difference between Horní and Dolní Ves rounded to the nearest meter? - Two artillery
Objective C we observe from two artillery observatories, A and B, which are 975 m apart. The size of the BAC angle is 63°, and the size of ABC is 48°. Calculate the distance of points A and C. - Ratio in trapezium
The ratio of the height v and the base a, c in the trapezoid ABCD is 1:6:3. Its area is 324 square cm, and the peak angle B is 35 degrees. Determine the perimeter of the trapezoid.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
