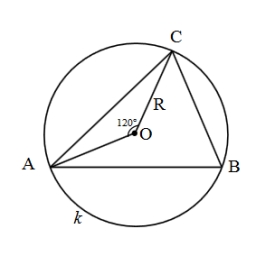
Circular railway
The railway connects points A, B, and C in a circular arc, whose distances are | AB | = 30 km, AC = 95 km, and BC | = 70 km. How long will the track be from A to C?
Correct answer:
Tips for related online calculators
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- planimetrics
- circle
- area of a shape
- perimeter
- triangle
- The Law of Cosines
- Heron's formula
- basic functions
- reason
- goniometry and trigonometry
- arccosine
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Track arc
Two straight tracks are at an angle 74°. They will join with a circular arc with a radius r=1127 m. How long will the arc be connecting these lines (L)? How far is the arc's center point from track crossings (x)? - Distances 79974
The picture shows three villages, A, B, and C, and their mutual air distances. The new straight railway line is to be built so that all the villages are the same distance from the line and that this distance is the smallest possible. How far will they be - Angle ASB
On a circle with a radius of 10 cm and with a center S, the points A, B, and C are given so that the central angle ASB is 60 degrees and the central angle ASC is 90 degrees. Find the length of the circular arc and the amount of AB and AC offsets. - Collinear lines
Points A, B, and C are collinear, and B lies between A and C. If AC = 48, AB = 2x + 2, and BC = 3x + 6, what is BC?
- Rail turn
The curve radius on the railway line is 532 m. The length of the rail track on it is 818 m. How many degrees is the angle ASB if A and B are boundary points and S is the center of the arc curve? - Rhombus construction
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides. - Determine 54881
On the tourist map with a scale of 1:50000, the section of the railway line between Bobrová Lhota and Javořiště is replaced by an arc of a circle with a radius of 6 cm. The arc is 90°. Determine the actual length of the track between the two villages.
